1. Развитие Международной температурной шкалы

В настоящее время шкала МТШ-90 является наиболее корректной аппроксимацией термодинамической температурной шкалы, и её замена не является необходимой срочной мерой. Переход на новую шкалу всегда сопряжен с экономическими и технологическими проблемами и поэтому должен быть полностью обоснован. Тем не менее со времени принятия МТШ-90 были разработаны и опробованы новые методы первичной и вторичной термометрии.

В настоящее время получили развитие акустическая, абсолютная радиационная, шумовая и другие термометрии, которые наряду с газовой имеют статус первичных. Поэтому в последние десятилетия научные исследования и дискуссии по совершенствованию МТШ проводятся в направлении:

1. применения этих термодинамических методов для определения и уточнения температур реперных точек, а в высокотемпературной области
2. расширения набора реперных точек.

Второе направление осуществляется за счет введения в шкалу точек фазовых переходов эвтектических сплавов металл-углерод для области температур выше 1300 °С .

Ещё в 1999 г. были предложены следующие точки, представляющие интерес для радиометрии и термометрии:

• NiС: 1326.5 °C ,
• PdС: 1504 °C ,
• PtС: 1705 °C ,
• RuС: 1940 °C ,
• FeС: 1153 °C ,
• CoC: 1320 °C ,
• RhC: 1694 °C ,
• IrC: 2296 °C ,
• ReC: 2505 °C ,
• OsC: 2732 °C .

В 2005 г Консультативный комитет по термометрии (ККТ) разработал специальный международный план исследований, ставящий целью значительно повысить точность измерения температуры высокотемпературных эвтектик выше точки затвердевания серебра.

Основные направления проводимых в настоящее время исследований следующие:

• выработка требований к чистоте материалов;
• разработка устройства ячеек реперных точек с гарантией воспроизводимости температуры ±500 мК ;
• исследование долговременной стабильности реперных точек и надежности ячеек;
• разработка конструкции печей с учётом влияния излучений;
• построение бюджета неопределенности для температур реперных точек;
• определение температур реперных точек металл-углерод абсолютными радиометрическими методами;
• проведение международные сличений выбранного набора реперных эвтектических точек с присвоением им значений термодинамических температур.

Постоянная работа по совершенствованию реализации термодинамической и практической температурной шкалы проводится Консультативным комитетом по термометрии (ККТ) в рамках общей работы Международного бюро по мерам и весам (МБМВ), структурным подразделением которого он является. Результатом многолетней работы явился концептуальный пересмотр основных единиц системы СИ, заключающийся в их отвязке от физических материальных носителей, таких, как эталон килограмма или метра, и выражение их через фундаментальные физические константы.

Окончательно это было принято в 2019 году. Эти кардинальные изменения коснулись и термометрии: было дано новое определение кельвина в его привязке к константе Больцмана k . При этом шкала МТШ-90 изменений не претерпела и остаётся официально действующей. Не изменились и числовые значения основных величин шкалы, таких, как температуры реперных точек, но в будущем их значение может быть изменено, если значение константы Больцмана k будет уточнено экспериментально и изменится. Необходимо заметить, что в настоящее время температуры реперных точек МТШ-90 являются точными, без заданной неопределенности, и фиксированными, то есть неизменными, пока действует шкала.

В 2002 г. в Чикаго в рамках международной конференции«Temperature, Its Measurement and Control in Science and Indusry» был проведен специальный семинар “Towards the ITS-XX” (К новой шкале МТШ-ХХ). Буквы ХХ означают возможную дату принятия шкалы.

2011 г. 17 – 21 октября 2011 г. в г. Севре под Парижем состоялось 24-е заседание Генеральной Конференции по Мерам и Весам. Конференция одобрила будущие предлагаемые изменения в определениях основных единиц СИ: кельвина, ампера, моля и килограмма (Резолюция №1).

Переход на новые определения единиц должен осуществляться осторожно. Никаких изменений повседневной жизни при этом не будет. Мало того, это не затронет течение обычных процессов в промышленности и других видах хозяйственной деятельности. Изменения определений немедленно скажутся только на самых точных, эталонных измерениях, проводимых в научных лабораториях. Лишь впоследствии, с возможным уточнением фундаментальных физических констант, может произойти корректировка каких-либо технологических или других подобных процессов, то есть – постепенно и без эксцессов.

Однако скорая реализация предложенных изменений в то время была невозможной. Никаких проблем с введением новых определений кельвина, ампера и моля не было, но большие сложности вызвало переопределение килограмма.

Теоретически было необходимо связать какую-либо очень точно измеренную фундаментальную константу с массой реального эталона (прототипа) килограмма. Затем числовое значение этой фундаментальной константы должно быть зафиксировано, и та же методика должна служить для измерения массы любых других объектов. При этом целевая неопределенность должна быть не хуже 20 мкг на килограмм, что в настоящее время может быть получено двумя способами.

Первый метод – сравнение массы прототипа килограмма и массы атома кремния.

Второй – метод «электоронных весов», который позволяет определить массу через постоянную Планка, В то время неопределённость постоянной Планка соответствовала 44 мкг на килограмм. Оба метода должны приводить к одинаковому результату. Таким образом, в то время корректно переопределить килограмм не представлялось возможным и завершение проекта перехода на новые определения единиц СИ планировалось лишь на 2014 г.

2014 г. На 25-м заседании Генеральной Конференции по Мерам и Весам был отмечен прогресс в определении физических констант и был утвержден стратегический план перехода на новое определение кельвина и других величин.

2018 г. 16 ноября 2018 года XXVI Генеральная конференция по весам и мерам (КГПМ) единогласно проголосовала за новые определения основных единиц СИ: килограмма, ампера, кельвина и моля. Единицы теперь определяются путем задания точных численных значений для постоянной Планка (h), элементарного электрического заряда (e), постоянной Больцмана (k) и постоянной Авогадро (Nа) соответственно.

2019 г. Новые определения основных единиц СИ: килограмма, ампера, кельвина и моля вступили в силу 20 мая 2019 года.

Необходимо заметить, что эти нововведения не бесспорны и имеют некоторую критику.

В том же году ККТ разработал документ по практической реализации единицы температуры, называемый «Mise en pratique for the definition of the kelvin in the SI» (MePK), то есть «Практическая реализация [французская часть названия] определения кельвина в системе СИ», который создаёт законодательную платформу для этого.

В данном документе кратко описываются методы первичной термометрии, а также практические температурные шкалы, которые позволяют реализовать кельвин с наилучшей точностью. Официальный перевод этих документов на русский язык пока отсутствует, но имеется перевод на портале в разделе сайта «Практическая реализация определения кельвина в системе СИ». MePK – это целый свод документов, включающий в себя тексты существующих практических шкал, технические приложения о реализации шкал МТШ-90 и ПНТШ-2000, описания первичных термометров и термодинамических методов измерения температуры, оценки отклонения термодинамической шкалы от практических.

Ещё в период разработки пересмотра основных единиц СИ ККТ создал целевую группу для работы над MePK, которая функционирует по настоящее время. Основным направлением деятельности этой группы является постепенное внедрение в практику новых подходов к использованию переопределённого кельвина, как одной из основных единиц СИ, и альтернативных термодинамических методов измерения температуры, получивших развитие за последнее время. Кроме этого, так как теперь единица температуры привязывается к константе Больцмана, группа следит за состоянием точности измерения этой константы и изучает положительные и отрицательные стороны введения нового определения кельвина.

2. Единица температуры – кельвин. Определение в МТШ-90 и современное определение

Определение кельвина в шкале МТШ-90. В основе определения было положено фиксированное значение температуры тройной точки воды и действовало до 20 мая 2019 г. (см. Глава 3, § 2). Единицей фундаментальной физической величины, термодинамической температуры, обозначаемой символом Т, является кельвин, обозначение К, который по определению точно равен 1/273,16 части термодинамической температуры тройной точки воды.

Напомним, что тройная точка воды – температура равновесия газообразной, жидкой и твердой фаз чистой воды (см. Глава 1, § 4). В шкале МТШ-90 для реперной точки ТТВ было добавлено (июнь 2005 г.) условие определённого изотопного состава:

• 0,00015576 моля 2Н на один моль 1Н
• 0,0003799 моля 17О на один моль 16О
• 0,0020052 моля 18О на один моль 16О.

Таким образом, единица температуры зависела от качества воспроизведения тройной точки воды, на стабильность температуры которой оказывает влияние, помимо изотопного состава, чистота самой воды и даже состав стекла ампулы ТТВ. Воду не только трудно очистить до высокой степени чистоты, но и поддерживать её в таком состоянии, в силу её высокой способности к растворению различных веществ. Даже из стекла в воду могут переходить микроколичества различных элементов.

Современное определение кельвина. Утверждено 16 ноября 2018 года на XXVI Генеральной конференции по мерам и весам и введено 20 мая 2019 с принятием изменений определений основных единиц СИ.

Кельвин, символ К, является единицей термодинамической температуры и определяется путем установления фиксированного числового значения постоянной Больцмана k равным 1,380649·10^–23 в единицах Дж / К (J / K) , что соответствует кг · м² · с^–2 К^-1, где килограмм, метр и секунда определены через константы h , c и Δv_Cs .

(Здесь h – постоянная Планка, c скорость света в вакууме и Δv_Cs – частота сверхтонкого расщепления основного состояния атома цезия- 133).

Точное выражение для кельвина в терминах определяющих констант k , h и Δv_Cs:

 

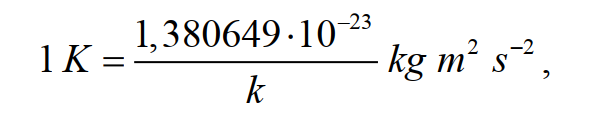
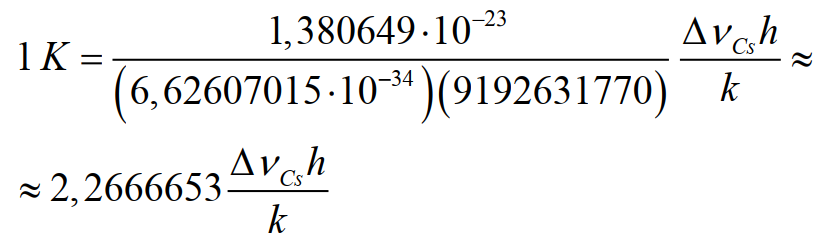
Из этого определения следует, что один кельвин равен изменению термодинамической температуры, приводящему к изменению тепловой энергии kT на 1,380649 ·10^–23 Дж.

Новое определение кельвина опирается на статистическую интерпретацию температуры, где термодинамическая температура – это мера средней тепловой энергии, приходящейся на степень свободы в системе. В этом плане естественной единицей термодинамической температуры являлся бы джоуль, но по историческим и практическим причинам кельвин остается основной единицей СИ. Также новое определение кельвина не отменяет практическое использование шкалы Цельсия с сохранением её связи с абсолютной шкалой.

В предыдущих практических температурных шкалах, в том числе в МТШ-90, передача единицы температуры почти во всех диапазонах так или иначе опиралась на значение ТТВ. Главным преимуществом введения нового определения кельвина является принципиальная возможность повышение точности температурных измерений вдали от тройной точки воды, в том числе – в высокотемпературной области.

Последнее сделает возможным независимое применение абсолютных радиационных термометров и ещё более приблизить практические измерения к термодинамической шкале. При этом можно будет избежать серьезных экономических и организационных трудностей, связанных с введением какой-то новой полноценной практической температурной шкалы. Ожидается, что со временем для некоторых диапазонов прямые термодинамические методы могут постепенно заменить МТШ-90, но в основе своей она ещё долго будет действовать.

В обозримом будущем в ключевом диапазон шкалы -200 ÷ 960 °С интерполяционным измерительным прибором попрежнему будет являться платиновый термометр сопротивления. Значения температур реперных точек останутся прежними, лишь немного изменятся неопределенности реперных точек, принятых на этапе подготовки МТШ-90. Последнее никак не скажется на практике измерения температур.

В настоящее время неопределенность экспериментального определением константы Больцмана составляет примерно 3,7 ·10^–7 , что соответствует неопределенности температуры ТТВ 0, 49 мК . В то же время воспроизводимость температуры ТТВ составляет примерно 0,05 мК , поэтому привязка кельвина к константе Больцмана не может в обозримом будущем повлиять на значение 273,16 К . Стандартная неопределенность температуры ТТВ теперь равна 0,1 мК.

3. Практическая реализация определения кельвина в системе СИ

Реализация переопределения кельвина на практике сводится к расширению методов первичной термометрии и, следовательно, к уточнению параметров практических температурных шкал и сближению их со шкалой термодинамической. Показания первичных термометров могут быть непосредственно переведены в температуру с использованием известных физических соотношений, таких как уравнение состояния. Эти термометры очень сложны в устройстве и требуют высококвалифицированного обслуживания.

К повсеместному практическому использованию они непригодны. С другой стороны, вторичные термометры имеют сравнительно простое устройство, но их показания (например, выходной электрический сигнал или длина столбика термометрической жидкости) непосредственно не связаны с температурой и такие термометры требуют градуировки по первичным. Передача единицы температуры вторичным эталонным термометрам, таким, как платиновые термометры сопротивления, производится с помощью температурных шкал (в настоящее время – МТШ-90) без непосредственного сличения с первичными. Важнейшую роль в этом играют реперные точки.

Абсолютная первичная термометрия позволяет измерять термодинамическую температуру непосредственно на основе определения единицы температуры – кельвина, что требует только знания числового значения постоянной Больцмана. При этом не требуется привязки к какой-нибудь фиксированной точке температуры и все параметры, входящие в уравнение состояния, измеряются или определяются независящим от температуры способом. Как уже указывалось ранее, первичными термометрами являются газовые и другие термодинамические измерители, получившие своё развитие за последнее время.

Относительная первичная термометрия позволяет измерять термодинамическую температуру косвенно, в фиксированных температурных точках, значения температуры которых определены методами абсолютной первичной термометрии. Таковыми точками являются реперные точки температурных шкал. Они должны обладать высокой воспроизводимостью и стабильностью. Использование новых методов абсолютной первичной термометрии позволяет расширить набор реперных точек прежде всего в высокотемпературной области, что является очень важным. Таким образом, вторичные эталонные термометры градуируются методами относительной первичной термометрии, что позволяет значительно снизить общую трудоёмкость термометрических операций.

Переопределение кельвина, описанное выше, не влияет на статус шкал МТШ-90 и ВНТШ-2000, но позволяет повысить точность измерения термодинамической температуры ниже 20 К и выше 1300 К при использовании первичных термометров. При этом ККТ рекомендует соответствующие первичные методы, отвечающие определённым критериям, таким как:

• применимость методов в требуемых температурных диапазонах;
• достаточно хорошее описание методов для обеспечения возможности их сторонней реализации;
• проведение сравнительных измерений с уже существующими методами;
• наличие полного обоснованного бюджета неопределенностей;
• полученная полная неопределённость может быть больше существующей в настоящее время не более чем на порядок (с перспективой дальнейшего улучшения).

4. Практическая реализация определения кельвина методами акустической газовой термометрии

В первичной акустической газовой термометрии используется выражение скорости звука u в идеальном газе (аналог уравнения (8)):

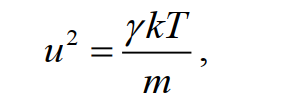
где k – постоянная Больцмана, m – средняя масса молекулы газа, γ – отношение теплоемкости газа при постоянном давлении к его теплоемкости при постоянном объеме (показатель адиабаты). Для идеального одноатомного газа γ = 5 / 3.

Абсолютная первичная акустическая газовая термометрия. «Формула скорости звука выводится из резонансных частот одноатомного газа, содержащегося в изотермической полости. Для точного определения резонансных частот необходимо использовать невырожденные акустические моды, и часто для этой цели используются невырожденные моды радиально-симметричных сферических полостей.

Средний радиус резонатора часто определяют с помощью микроволновых резонансов. Неидеальные свойства реальных газов компенсируются посредством усложнения соотношения для скорости звука и экстраполяции его к нулевому давлению. Измерения частот акустического резонанса, давления, размеров полости и молекулярной массы газа должны метрологически прослеживаться к метру, килограмму и секунде. Первичная акустическая газовая термометрия была реализована при температуре тройной точки воды с относительными неопределенностями порядка 10-6 . Однако такая низкая неопределенность еще не подтверждена независимыми измерениями».

Относительная первичная акустическая газовая термометрия «основана на определении отношений термодинамических температур из отношений скоростей звука. Обычно результат измерения получают относительно реперной точки, для которой уже известна термодинамическая температура. Измеренное отношение температур обычно выражаются в виде измеренных отношений длин и частот звука. Метод относительной первичной акустической газовой термометрии был реализован в широком диапазоне температур от нескольких кельвинов до 550 К . Независимые реализации этого метода обычно совпадают в пределах 3·10^-6 T в диапазоне от 234 K до380 K ».

5. Практическая реализация определения кельвина методами спектральной радиометрии

Первичная спектральная радиометрия применяется для диапазона температур 1235 К и выше.

Основным уравнением выступает закон Планка, выражающий зависимость спектральной яркости L_b,λ идеального абсолютно черного тела от температуры:

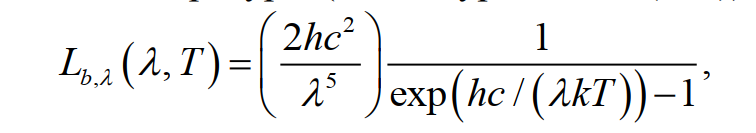
где k – константа Больцмана, h – постоянная Планка, c – скорость света в вакууме, λ – длина волны в вакууме. Спектральная яркость определяется как мощность излучения на единицу площади, на единицу телесного угла, на единицу длины волны и выражается в единицах Вт·м^–2ср^–1нм^–1 (ср – стерадиан).

Абсолютная первичная радиометрия  «требует точного определения оптической мощности, излучаемой в известной спектральной полосе и известном телесном угле изотермической полостью с известной излучательной способностью. Для измерения мощности необходим радиометр, состоящий из детектора и спектрального фильтра с известной абсолютной спектральной чувствительностью.

Оптическая система обычно включает два совмещенных друг с другом круглых отверстия, разделенных заданным расстоянием, определяющим телесный угол, и может дополнительно включать линзы или зеркала. Также должен быть известен показатель преломления среды, в которой производится измерение. Все измерения задействованных величин должны прослеживаться до соответствующих единиц СИ, в частности, ватта и метра. Возможные неопределенности первичной радиометрии около 0,1 К ( k = 1) при 2800 К ».

Также ККТ разработаны практические рекомендации по реализации абсолютной первичной радиометрической термометрии и оценки неопределенности.

Относительная первичная радиометрия не требует знания ни абсолютной спектральной чувствительности радиометра, ни количественной оценки геометрических факторов, определяющих телесный угол. Здесь измеряется мощность излучения относительно излучения реперных черных тел, термодинамическая температура которых уже известна.

Существует три общепризнанных подхода к относительной первичной термометрии:

• экстраполяция от одной реперной точки, которая требует только знания относительной спектральной чувствительности детектора и фильтра;
• интерполяция или экстраполяция от двух реперных точек, которая требует только знания ширины полосы чувствительности;
• интерполяция или экстраполяция от трех или более реперных точек, которая не требует детального измерения чувствительности.

Интерполяция и экстраполяция значительно упрощаются с использованием хорошо изученной параметрической аппроксимации интегрального выражения для оптической мощности (например, с помощью формы Планка уравнения Сакумы – Хаттори), что устраняет необходимость итеративно решать интегральное уравнение, описывающее измеренную оптическую мощность. Относительная первичная радиометрия дает неопределенности, которые лишь немного выше, чем абсолютная первичная радиометрия.

6. Практическая реализация определения кельвина методами поляризационной газовой термометрии

Поляризационная газовая термометрия основана на измерении давления газа p и его электрических и магнитных параметров – молярной электрической поляризуемости Aε , молярной магнитной поляризуемости Aμ , диэлектрической постоянной (диэлектрической проницаемости) ε_r , а также показателя преломления n . С температурой эти величины могут быть связаны с помощью уравнений Клаузиуса-Моссотти и Лоренца-Лоренца . В первоначальную форму этих уравнений входит плотность газа, которая, после комбинирования с уравнением состояния идеального газа (5) заменяется давлением.

Уравнение Клаузиус-Моссотти будет иметь вид:

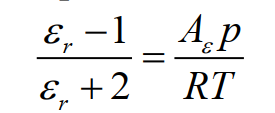(3)

а уравнение Лоренца-Лоренца преобразуется к:

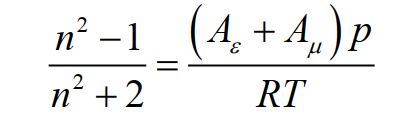(4)

ε_r может быть легко определена по измерениям электрической ёмкости газа, n – посредством измерения частот микроволнового резонанса; Aε и Aμ для разреженных газов практически не зависят от температуры и могут быть предварительно измерены при температурах нескольких реперных точек; существуют также методы точного измерения давления p . При ненулевых плотностях уравнения Клаузиуса-Моссотти и Лоренца-Лоренца всё же отклоняются от идеальности, поэтому для снижения погрешности используется разложение в степенной ряд с вириальными коэффициентами. Для поляризуемости требование неопределенности менее 1 ppm в настоящее время выполняется только для гелия ( Aε ≈ 0,52 см3 / моль и Aμ ≈ 0, 0000079 см3 / моль ).

Термометрия на основе диэлектрической постоянной газа.

Диэлектрическая постоянная газа ε_r теоретически равна отношению ёмкости конденсатора с газом C(p) к ёмкости конденсатора в вакууме C(0) . Однако в действительности изменение давления будет менять геометрию электродов конденсатора; учёт этого и других факторов приводит к эмпирическому уравнению для определения ε_r , которое удовлетворительно описывает эту зависимость:

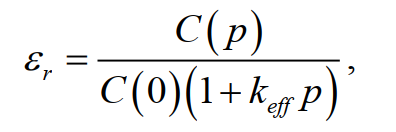(5)

k_eff – отрицательная эффективная изотермическая сжимаемость.

Измерения ёмкости принципиальных трудностей не представляют, но в нашем случае требуется применение прецизионного ёмкостного моста, сравнимого с эталонным, поскольку значение Aε для гелия мало. Уравнение комбинируют с соотношением между ε_r и p, измеряют изотермы C = f(p) для нескольких температур и экстраполируют результаты для предельного случая идеального газа.

Необходим также расчёт величины k_eff , которая зависит от индивидуальных упругих постоянных конструкционных материалов измерительного конденсатора. При такой методике не требуется знание вириальных коэффициентов и значения термодинамической температуры T могут быть определены.

«Первичная газовая термометрия по диэлектрической постоянной была проведена в тройной точке воды с относительной неопределенностью порядка 1 ppm. Относительная неопределенность результатов в низкотемпературном диапазоне уменьшается от примерно 40 ppm при 2,5 К до примерно 10 ppm при 100 К . Все результаты подтверждены независимыми термодинамическими измерениями в пределах заявленной неопределенности».

Газовая термометрия на основе показателя преломления.

«В случае абсолютной первичной микроволновой термометрии показатель преломления определяется посредством измерения частот микроволнового резонанса fm(p) изотермической полости, заполненной газом (индекс «m» указывает конкретную микроволновую моду.) Обычно используются квазисферические или цилиндрические формы резонатора, причем размеры полости при рабочем давлении газа рассчитываются с учетом положительной изотермической эффективной сжимаемости k_eff корпуса резонатора на основе резонансных измерений, выполненных в вакууме fm(0) (знак k_eff  зависит от конструкции резонатора):

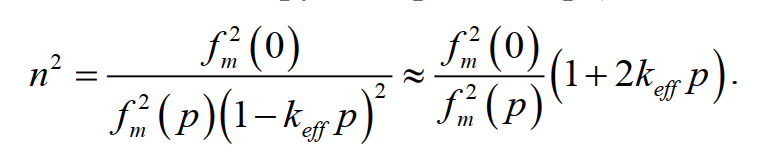(6)

Это эмпирическое уравнение для определения n2 аналогично уравнению (5), причем влияние отрицательной эффективной сжимаемости k_eff вдвое больше. Уравнение содержит отношение частот микроволнового резонанса f²_m(0) / f²_m (p). Это отношение можно точно измерить, используя часы, которые стабильны в течение интервала, необходимого для проведения термически уравновешенных измерений fm(0) и fm(p) (для изотермы обычно это дни или недели).

Для вывода полного рабочего уравнения газовой термометрии по показателю преломления уравнение (6) должно применяться в сочетании с соотношением (4). Кроме того, для описания свойств реального газа гелия, должны использоваться степенные ряды с различными вириальными коэффициентами, как для уравнения Лоренца-Лоренца, так и для уравнения состояния. Применяя полное рабочее уравнение и измеряя изотермы n2 в зависимости от p при различных температурах, можно с помощью экстраполяции получить результаты для предельного состояния идеального газа. В этом предельном случае значения вириальных коэффициентов не нужны и, таким образом, может быть вычислена термодинамическая температура T .

Также, как и в предыдущем методе, требуется расчёт эффективной сжимаемости измерительного конденсатора, зависящей от индивидуальных упругих постоянных конструкционных материалов.

Абсолютный первичный термометр по показателю преломления был реализован с использованием газообразного гелия при температуре тройной точки воды с относительной неопределенностью порядка 10 ppm , а при температурах тройных точек неона, кислорода и аргона, – с относительной неопределенностью порядка 20 ppm . Все результаты подтверждены независимыми термодинамическими измерениями в пределах оцененной неопределенности».

7. Практическая реализация определения кельвина методами шумовой термометрии Джонсона

Принцип первичной шумовой термометрии Джонсона. Термометрия электрических шумов основана на теореме флуктуации-диссипации, которая описывает тепловое возбуждение носителей заряда внутри электрического проводника. Спектральная плотность мощности шумового напряжения V на резисторе с электрическим импедансом Z f (комплексная величина), выражается как:

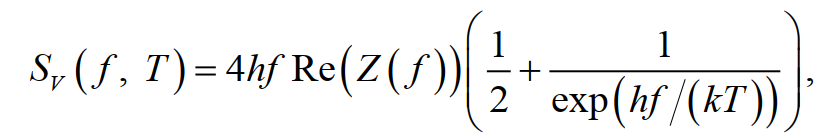(7)

где f – частота, T – термодинамическая температура, h – постоянная Планка, k – постоянная Больцмана, а функция Re означает действительную часть числа. Импеданс, – полное сопротивление переменному току, включает в себя ёмкостную и индуктивную составляющую, но может быть и просто активным сопротивлением Re(Z(f)) = R , когда остальные две составляющие практически равны нулю. Если пренебречь квантовыми поправками при условии hf , это уравнение сводится к формуле Найквиста :

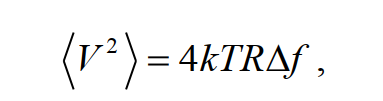(8)

где Δf – полоса пропускания, в которой измеряется шумовое напряжение. Квантовые эффекты могут вносить относительную поправку, равную (hf / kT)² / 12 , которая составляет, например, 2 ·10^–10 при 1 мК и 1 кГц или менее чем 2 ·10^–9 для температур около 300 К и частот ниже 1 ГГц .

Абсолютная первичная низкотемпературная шумовая термометрия Джонсона (ниже 4 К).

Эта методика «при низких температурах требует измерения спектральной плотности мощности на источнике шума с точно известным импедансом Z f , который обычно зависит от частоты.

Источник шума, как правило, изготавливается из металла высокой чистоты, содержащего незначительное количество магнитных примесей для обеспечения независимого от температуры импеданса. При низких температурах шумовые сигналы очень слабые и в большинстве случаев измеряются датчиком на основе устройства сверхпроводящей квантовой интерференции SQUID. В оцениваемой полосе частот электронная передаточная функция всей цепи, включающая источник шума и датчик SQUID, должна быть точно определена. Относительные суммарные стандартные измерения термодинамической температуры с помощью метода абсолютной первичной низкотемпературной шумовой термометрии составили величину порядка 1·10^–3 .

Относительная первичная низкотемпературная термометрия шума Джонсона (ниже 4 К).

«В относительных первичных низкотемпературных шумовых термометрах отношения температур определяются из отношения измеренной спектральной плотности мощности шума к спектральной плотности мощности шума опорной температурной точки, для которой известно термодинамическое значение температуры. Неопределенность этого метода может быть того же уровня или ниже, что и для абсолютной первичной низкотемпературной шумовой термометрии, при условии, что неопределенность термодинамической температуры опорной точки достаточно низкая».

Абсолютная первичная шумовая термометрия Джонсона (выше 1 К).

«Спектральная плотность мощности шума выводится из измерений среднеквадратического напряжения шума (или шумового тока) в пределах полосы пропускания измерительной системы, а также из измерения сопротивления. Неидеальные свойства переменного тока реальных резисторов и соединительных проводов можно учесть с помощью частотно-зависимой модели и экстраполяции к нулевой частоте.

Измерения напряжения, сопротивления и полосы пропускания должны метрологически прослеживаться до единиц СИ – ампера, килограмма и секунды. Эта методика при температуре тройной точки воды показала относительные неопределенности порядка 4·10^–6.

Точные электронные измерения были выполнены путем сравнения мощности теплового шума с мощностью волнового псевдослучайного шума, генерированного с помощью волнового сверхпроводящего джозефсоновского синтезатора. Низкие погрешности, заявленные для этого метода, были подтверждены независимыми измерениями с использованием абсолютной первичной акустической газовой термометрии».

Относительная первичная шумовая термометрия Джонсона (выше 1 К).

Методика «основана на определении отношения термодинамических температур по измеряемым отношениям спектральных плотностей мощности. Обычно температура определяется по отношению к температуре опорной точки, для которой известна термодинамическая температура. Измеренные отношения температур выражаются в терминах измеренных отношений мощности шума и сопротивления. Относительная первичная шумовая термометрия была реализована в широком диапазоне температур до 2500 K ».