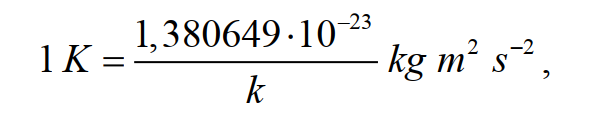Содержание страницы
1. Введение
Температура является одной из семи основных величин Международной системы единиц СИ (остальные – масса, длина, время, сила электрического тока, сила света и количество вещества). Из них по крайней мере четыре – масса, длина, время и температура, – непосредственно связаны с человеческой деятельностью и воспринимаются интуитивно.
Температура даже на бытовом уровне всегда связывается со степенью нагретости тел и способностью их обмениваться теплотой. При этом температура выступает как одно из свойств тела, которое обусловливает возможность изменения его энергетического состояния за счёт передачи или принятия теплоты (тепловой энергии).
В плане этого весьма удивительно то, что в науке температура практически оставалась непонятой вплоть до XVIII века, а более-менее приемлемое определение температуры было дано ещё век спустя.
Одной из главных причин этого было то, что понятие температуры часто путали с теплотой, особенно после введения в науку теории теплорода (Лавуазье, 1783 г.), – то есть флюида, нечто вроде невесомой текучей жидкости, которая и определяет степень нагретости тел и способна «перетекать» от тела к телу. То есть температура не связывалась со свойствами самого тела, с движением микрочастиц, его составляющих. Эта теория просуществовала до начала XIX века и была экспериментально опровергнута Бенджаменом Томпсоном (графом Румфордом) (1798 г.) и Хэмфри Дэви (1799 г.), которые связали теплоту с движением частиц. Это, в частности, способствовало принятию в середине XIX века молекулярно-кинетической теории, которая, в свою очередь, позволила к 1887 году впервые унифицировать количественные методы измерения температуры.
В настоящее время трудно переоценить роль контроля и измерения температуры во всех отраслях народного хозяйства, в науке, в быту. В советское время, по оценкам экспертов, измерения температуры составляли около 30% всех измерений, проводимых в народном хозяйстве, а значение температурных измерений практически во всех областях естественных наук общеизвестно. Особенно всё вышесказанное относится к химическим и химико-технологическим производствам и соответствующим областям науки, так как температура является важнейшим фактором, действующим на химические реакции и физико-химические процессы.
2. Понятие температуры
Научное обоснование температуры, как параметра состояния термодинамической системы, даётся на основе нулевого закона термодинамики (закона транзистивности термического равновесия):
Если каждая из двух систем находится в состоянии теплового равновесия с третьей, то они находятся в тепловом равновесии друг с другом. При этом системы находятся в тепловом контакте с третьей и отсутствует теплоизоляция.
(Напомним, что этот закон получил такой номер потому, что был введён после (постулат Афанасьевой, Т. А. Афанасьева-Эренфест s5, 1925 г.; постулат Фаулера, Р. Г. Фаулер s6, 1931 г.) первого, второго и третьего законов термодинамики, но по смыслу и логике должен стоять первым).
Равновесие характеризуется, прежде всего, отсутствием каких-либо макроскопических процессов; тепловое (термическое) равновесие характеризуется отсутствием теплопередачи.
Тепловой контакт подразумевает непосредственное соприкосновение систем (или тел), когда составляющие их микрочастицы могут взаимодействовать друг с другом и передавать свою энергию движения.
Теплоизоляция означает, что при тепловом контакте одна из систем имеет крайне низкую теплопроводность (способность проводить теплоту) или на границе раздела имеется третья система, прослойка, с такой низкой теплопроводностью. Эта система также ещё называется адиабатической оболочкой.
Иллюстрация закона дана на рис. 1. В тепловом контакте находятся системы I и II, II и III, а системы I и III непосредственно не соприкасаются, но, по нулевому закону, находятся в тепловом равновесии друг с другом. Следовательно, должен существовать параметр состояния, одинаковый для всех трёх систем; такой параметр отождествляется с температурой. Таким образом, температура, это параметр состояния термодинамической системы (то есть – одно из свойств), определяется только самим состоянием и не зависит от пути перехода системы в него (от предистории).
Температура – величина интенсивная, то есть она самопроизвольно выравнивается в системе. Поскольку, как мы позднее увидим. температура сравнительно легко измеряется, она всегда выступает в качестве параметра, а не функции состояния.
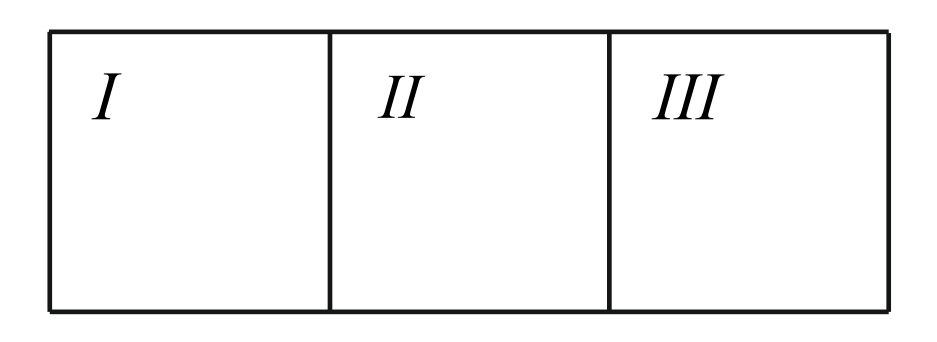
Рис. 1. Иллюстрация нулевого закона термодинамики. I, II, III – термодинамические системы
Из рис. 1 также следует принцип измерения температуры: систему II можно считать абстрактным термометром, который сначала приводится в тепловой контакт с системой I, а затем – с системой II; если термометр покажет одинаковую температуру, то системы I и II находятся в тепловом равновесии, а если – разную, то мы можем судить о том, насколько отличаются их тепловые состояния.
При этом обосновывается так называемая эмпирическая температура, то есть температура, которая может быть измерена тем или иным, конкретным термометрическим телом.
Нулевой закон термодинамики достаточно очевиден и иногда высказываются сомнения в целесообразности его существования. Однако температура и её обоснование совершенно необходимы для полного описания макросистем уже на этапе интерпретации первого закона термодинамики. Поэтому в формальной феноменологической термодинамике нулевой закон должен занимать своё место.
3. Обоснование температурных измерений
При измерении эмпирической температуры абстрактный термометр (система II, описанная в предыдущем параграфе) не может служить простым инструментом сравнения, как это следует из рис. 1, так как, во-первых, пришлось бы каким-то образом контролировать отсутствие теплопередачи (что само по себе сложная задача), а вовторых, мало что давало бы, так как зафиксировать можно было бы только или равенство, или неравенство эмпирических температур систем I и III.
Чтобы получить практически значимый термометр, необходимо использовать следующую схему измерения: сначала термометр приводится в тепловое равновесие с системой I (выдержкой по времени) и фиксируется какое-то физическое свойство абстрактного термометра, как термометрического тела, а затем то же самое делается для системы III. Если выбранное физическое свойство окажется одинаковым, то температуры систем I и III одинаковы, если – нет, то по разности величин этого физического свойства можно будет судить о разности температур. При этом необходимо построить соответствующую шкалу, и тогда будет получен прибор, универсальный для всех возможных систем.
Однако здесь сразу проявляется одна из главных трудностей измерения эмпирической температуры – зависимость измерений от свойств термометрического тела. Как показывает опыт, практически не существует свойств тел или систем, линейно зависящих от температуры. Многие свойства являются нестабильными для одних и тех же веществ, или одни и те же свойства могут несколько отличаться для, казалось бы, одного и того же вещества (например, в зависимости от способа получения, загрязнённости, несовершенств внутреннего строения твёрдых тел и т. д.).
Вторая главная трудность (но, пожалуй, первая по значимости) лежит в общетеоретической области. Из всех 7 основных физических величин только температура является интенсивным (выравнивающимся) свойством, остальные – экстенсивные (суммирующиеся). Напомним, что экстенсивные свойства зависят от количества вещества в системе; если систему, например, удвоить, то масса системы возрастёт вдвое, если время удвоить, то мы получим отрезок времени, в два раза больший. А вот температура не изменится при удвоении системы, и это приводит к сложностям при построении измерительных схем.
Поясним это на следующем примере. Чтобы создать практически применимую схему измерения, например, массы, можно, грубо говоря, взять любой кусок любого твёрдого вещества, объявить его эталоном и использовать с помощью весов, изготовив гири из кратных частей этого «эталона».
Конечно, на самом деле всё гораздо сложнее, необходимо обеспечить высокую стабильность массы эталона, то есть независимость её от времени, воспроизводимость его, то есть возможность изготовления вторичных эталонов той же массы и их кратных частей и так далее. В итоге мы имели эталон массы, использовавшийся до недавнего времени, изготовленный из специального сплава по соответствующей технологии, и хранящийся со всеми предосторожностями – рис. 2, 3. Однако никаких принципиальных трудностей это не составляет и всё сводится к описанной выше схеме использования.

Рис. 2-а. Международный прототип (эталон) килограмма хранится в Международном бюро мер и весов (расположено в Севре близ Парижа) и представляет собой цилиндр диаметром и высотой 39,17 мм из платино-иридиевого сплава (90 % платины, 10 % иридия).

Рис. 2-б.

Рис. 3. Копия эталона 1 кг, хранится в США.
Всё гораздо сложнее в случае измерения температуры. Мы можем подобрать какую-то физико-химическую систему или процесс, при котором температура будет с высокой точностью фиксированной (об этом будет рассказано ниже) и приписать этой температуре какое-то «эталонное» значение. Однако, если мы возьмём две такие системы, температура не увеличится в два раза. Таким образом, необходимо иметь несколько разных опорных (реперных) температур и построить соответствующую шкалу, выбрав единицу температуры. Такая шкала должна быть высокостабильна, а единица температуры, кроме этого, должна быть воспроизводима с высокой точностью и переносима на другие системы.
Рассмотрим следующий пример. Всем хорошо известен стеклянный ртутный термометр (рис. 4). Существуют как бытовые, так и высокоточные лабораторные приборы. В использовании они крайне просты, имеющиеся шкалы уже проградуированы в единицах температуры. Однако, если задуматься, можно увидеть, что о температуре мы судим по длине столбика ртути (термометрическое тело) в капилляре.
Но длина не является температурой, и имеющаяся шкала должна была быть каким-то образом построена и соотнесена с температурой. При этом, чтобы разные термометры соответствовали одной и той же шкале, необходимо, чтобы внутренний диаметр капилляров был строго одинаков как для одного капилляра по высоте, так и для капилляров разных термометров, а показатели чистоты ртути были одни и те же.
Исторически сложилось так, что первые практически значимые шкалы температур были построены как раз на основе жидкостных термометров. При этом, как правило, выбирались две опорные (реперные) точки, температура которых соотносилась с показаниями конкретного термометра, а длина столбика ртути делилась на какое-то число частей (например, в шкале Цельсия – интервал от температуры замерзания воды до температуры кипения делился на 100) и одна часть принималась за единицу температуры – градус. Таким образом, выбор единицы измерения был произвольным, так же, как и в случае экстенсивных величин, но всё же опирался на температуру реперных точек. Для экстенсивных же величин такой выбор был произволен абсолютно.
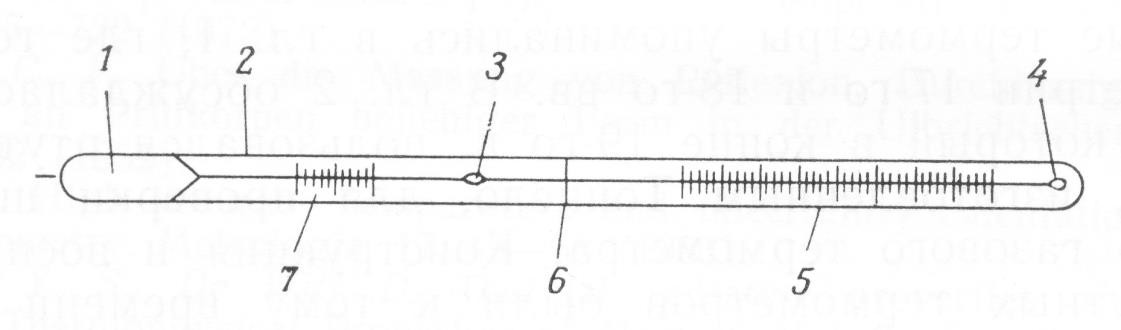
Рис. 4. Схема ртутного термометра. 1 – резервуар со ртутью; 2 – стеклянный корпус; 3 – камера сжатия (может отсутствовать); 4 – расширительная камера; 5 – основная шкала; 6 – отметка глубины погружения (может отсутствовать); 7 – вспомогательная шкала (может отсутствовать).
Что касается ртутных термометров, выбор термометрического тела был не случаен, так как в достаточно узком диапазоне температур полученную для ртути шкалу можно было считать равномерной с достаточной точностью. Это было вполне допустимо для бытовых, технических и рабочих термометров, однако при прецизионных измерениях неравномерность шкалы всё-таки становится заметной и в соответствующих эталонных термометрах шкала немного неравномерна, особенно для диапазонов шире, чем упомянутые две реперные точки. Такие неравномерные шкалы создавались уже после принятия градуса по равномерной шкале.
4. Принципы построения шкалы по реперным точкам
Из сказанного выше следует важность правильного выбора реперных точек. Они должны обладать высокой стабильностью и воспроизводимостью соответствующей температуры.
За многие десятилетия практики термометрических измерений были выбраны два вида подходящих систем: 1) фазовый переход жидкость – твёрдое тело и 2) системы с тройной точкой. Третьим важнейшим фактором явилось теоретическое обоснование (с косвенным экспериментальным подтверждением) существования 3) абсолютного нуля температур.
1. Фазовый переход жидкость – твёрдое тело и жидкость – газ. Фазовые переходы первого рода с изменением агрегатного состояния вещества считаются равновесными, если они протекают достаточно медленно. Типичная кривая (качественный график) охлаждения жидкости с фазовым переходом в твёрдое состояние представлена на рис. 5.
Из рис. 5 видно, что с течением времени жидкость медленно (чем медленнее, тем процесс ближе к равновесному) охлаждается, и её температура падает вплоть до температуры затвердевания (кристаллизации), после чего начинается постепенное выпадение твёрдой фазы.
Температура при этом не меняется. Нужно заметить. что температура затвердевания равна температуре плавления, а направление процесса (затвердевание или плавление) определяется действием окружающей среды, то есть направлением теплового потока. На кривой охлаждения наблюдается горизонтальная площадка, длина которой определяется массой данного индивидуального вещества. После полного затвердевания образца температура системы опять начинает понижаться, но уже с другой скоростью (наклоном кривой).
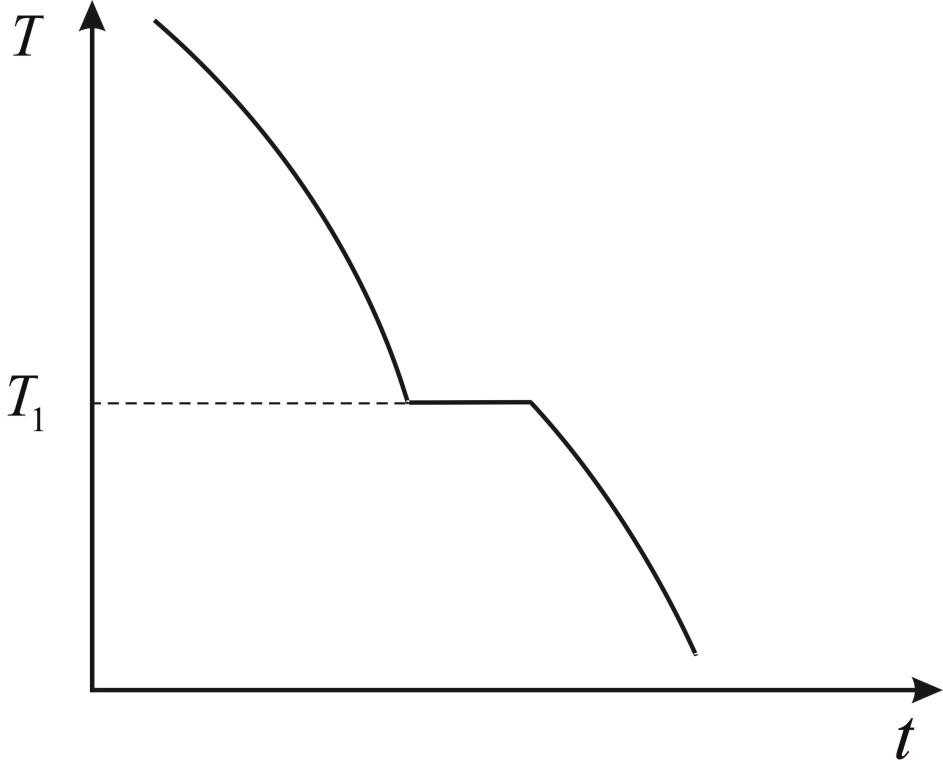
Рис. 5. Типичная кривая охлаждения жидкости с фазовым переходом в твёрдое тело. T – температура; T1 – температура затвердевания (она же – температура плавления); t – время.
Реальные кривые охлаждения имеют закруглённые углы, ниспадающие линии представляют собой кривые, хотя и близкие к прямым, а площадки имеют очень небольшой наклон, так как процесс не на 100% равновесный и при фазовом переходе имеется температурный градиент по объёму образца (рис. 6).
Наиболее удобными системами для температурных измерений являются чистые металлы, вода и некоторые другие вещества. Температуры затвердевания очень слабо зависят от внешнего давления (а в метрологии к тому же используются металлы в закрытых ампулах) и хорошо воспроизводятся.
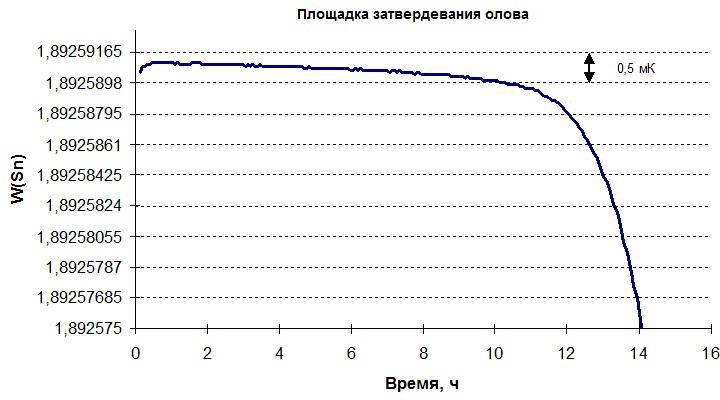
Рис. 6. Реальная кривая охлаждения чистого олова (участок фазового перехода в увеличенном масштабе)
На ранних этапах развития термометрии в качестве реперной использовалась точка замерзания воды при нормальном давлении p = 101325 Па = 760 Торр = 1 атм, однако позднее она была заменена на более удобную тройную точку воды с температурой выше примерно на 0,00993 K. Температура же замерзания воды остаётся нулевой точкой шкалы Цельсия и составляет по определению 273,15 K .
В практике температурных измерений применяется также фазовый переход жидкость – газ, в частности, – для воды при внешнем давлении 1 атм . Однако температура кипения очень сильно зависит от внешнего давления и загрязнения образца (например, вода при повышенных температурах сильнее растворяет возможные примеси). По факту точность воспроизводства этих реперных точек ниже, чем для систем с фазовым переходом жидкость – твёрдое тело, поэтому первые применяются только в качестве вторичных реперных точек (за исключением крайне низких температур).
2. Системы с тройной точкой. Тройной точкой называется точка на диаграмме состояния однокомпонентной системы, в которой одновременно сосуществуют три фазы: твёрдая, жидкая и газообразная. По правилу фаз Гиббса такая система будет инвариантна, то есть не будет иметь степеней свободы. Это означает, что такое состояние системы возможно только при строго определённых значениях давления и температуры, что крайне важно для термометрических измерений.
Напомним, что правило фаз Гиббса:
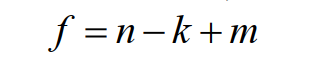 (1)
(1)
связывает между собой число компонентов n (в нашем случае n =1), количество фаз k ( k = 3), число внешних параметров, действующих на систему m (в нашем случае это давление и температура, то есть m = 2) и число термодинамических степеней свободы f , то есть количество независимых переменных (внешних параметров), которые можно произвольно (в некоторых пределах) менять без того, чтобы система претерпела качественные изменения (то есть без изменения числа фаз).
В нашем случае f = 0 и значения давления и температуры строго определены и изменены быть не могут. (В случае f = 1 и k = 2 произвольно можно изменить только один из двух параметров, а второй нужно будет изменить зависимым образом, чтобы в системе сохранились две фазы. В отличие от тройных точек это означает, что при использовании в качестве реперных точек, например, температуры кипения или плавления, необходимо фиксировать соответствующее давление).
В термометрии исключительную роль играет тройная точка воды – рис. 7, существующая при p = 611 Па = 4,58 Торр и T = 273,16 K (по определению). Следует отметить, что эта температура на 0, 01 К больше, чем температура плавления льда 273,15 K , по которой ранее строилась температурная шкала.
До недавнего времени (2019 г.) эта точка была основной реперной точкой и по ней определялась единица измерения температуры (кельвин). Считается, что это самая точно воспроизводимая реперная точка в термометрии (погрешность меньше милликельвина).
Подавляющее большинство основных и вспомогательных реперных точек также являются тройными для различных систем.
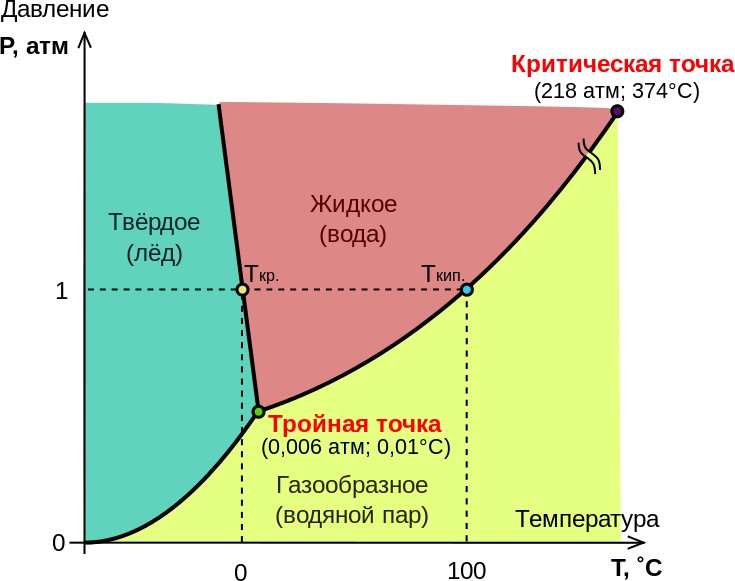
Рис. 7. Фазовая диаграмма воды (масштаб не выдержан)
3. Абсолютный нуль температур. Важнейшим этапом в становлении современной термометрии явилось косвенное экспериментальное подтверждение наличия абсолютного нуля температур. Впервые это было установлено, как одно из следствий экспериментов Гей-Люссака по изучению теплового расширения различных газов при постоянном давлении (атмосферном) в диапазоне температур от 0°C до 100°C . При этом измерялось относительное увеличение объёма газа (Vt — V0) / V0 с ростом температуры t по шкале Цельсия (здесь V0 – объём газа при начальной температуре t0 , в данном случае t0 = 0°C ). В результате был установлен закон:
Относительное изменение объема газа данной массы при постоянном давлении прямо пропорционально изменению температуры:
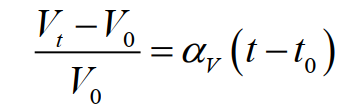 (2)
(2)
где αv – коэффициент теплового объёмного расширения; его смысл более понятен из преобразованной формулы:
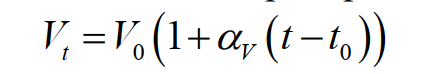 (3)
(3)
Этот коэффициент оказался почти одинаковым (разброс около 4%) для различных газов – табл. 1.
Таблица 1. Коэффициент теплового объёмного расширения αv , 1/К, для различных газов; усреднённый, для диапазона 0°C – 100°C .
| Воздух | 0,003671 |
| Водород | 0,003661 |
| Окись азота | 0,003720 |
| Циан | 0,003877 |
| Углекислый газ | 0,003710 |
| Угарный газ | 0,003669 |
| Оксид серы | 0,003903 |
Из формулы (3) видно, и это подтверждает эксперимент, что зависимость Vt = f (t) прямо пропорциональная. Если экстраполировать эту зависимость влево, до пересечения с осью абсцисс (то есть с осью t ), то мы получим некую температуру, при которой объём газа сожмётся до 0 (гипотетически), то есть газ не может иметь более низкую температуру (рис. 8).
Из (2):
 (4)
(4)
При опорной температуре t0 = 0°C в точке пересечения с осью абсцисс имеем Vt = 0, тогда для водорода по результатам Гей-Люссака:
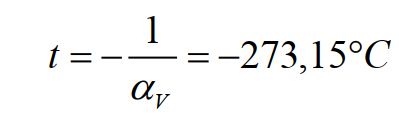 .
.
Это в точности совпадает со значением абсолютного нуля температур, принятым в настоящее время! Такое хорошее совпадение объясняется тем, что водород – практически идеальный газ при этих условиях. Гей-Люссак же нашёл среднее значение αv для своих результатов и получил t = -267,06°C . Сейчас то мы понимаем, что усреднять эти значения смысла не имело.
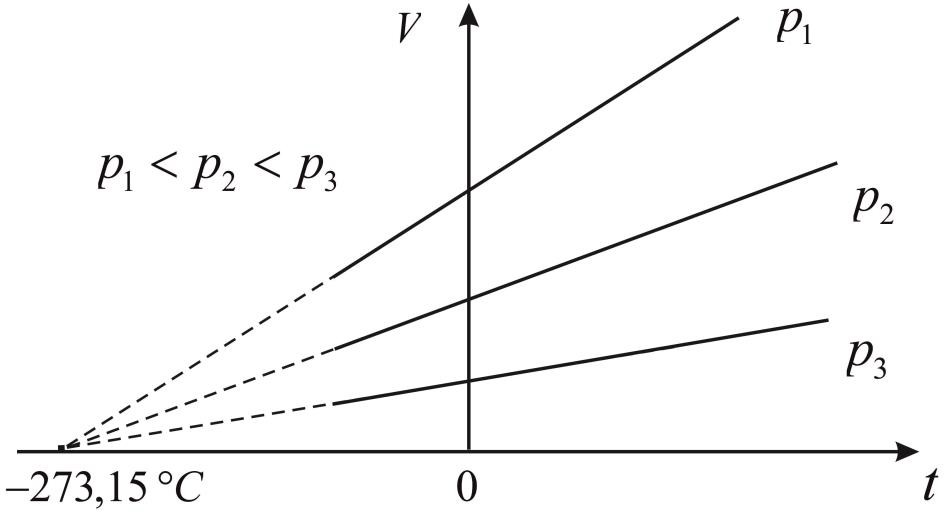
Рис. 8. Зависимость объёма газа от температуры при различных давлениях (штриховые линии – экстраполяция)
Необходимо отметить, что ещё до Гей-Люссака Алессандро Вольта провёл похожие опыты и получил значение t = -270°C , однако эти результаты оставались долгое время малоизвестными. Далее выяснилось, что αv для одного и того же газа несколько меняется с давлением; при увеличении давления прямая смещается вниз (в соответствии с законом Бойля-Мариотта s10, s11) и её наклон меняется так, что при экстраполяции все прямые сходятся в одной точке -273,15°C (рис. 8).
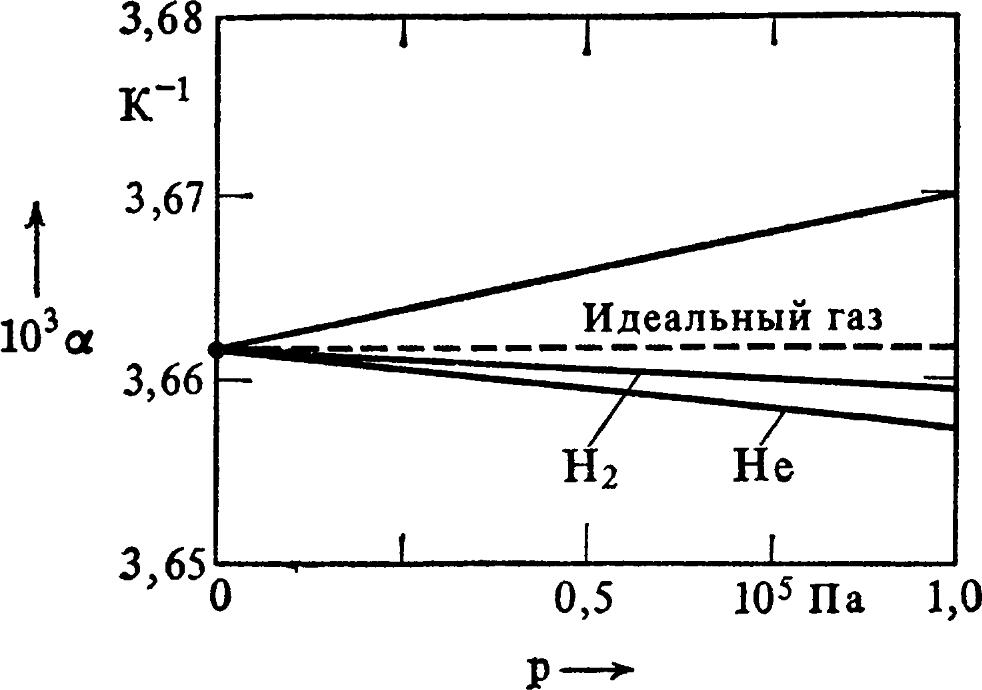
Рис. 9. Зависимость усреднённых коэффициентов расширения различных газов от давления (верхняя прямая – воздух)
Значительно позднее были проведены эксперименты по определению αv в зависимости от давления для различных газов – рис. 9.
Таким образом, было обосновано существование абсолютного нуля температур в рамках представлений об эмпирической температуре. В дальнейшем его существование было подтверждено теоретически с позиций термодинамики. Использование его при построении температурной шкалы было предложено ещё Амонтоном, а позднее – строго обосновано лордом Кельвином. В качестве второй реперной точки используется тройная точка воды.
5. Первичная и вторичная термометрия
Поскольку температура является интенсивным свойством, то, как уже отмечалось, главной задачей измерения эмпирической температуры является поиск таких систем в качестве термометрического тела, при использовании которых изменение соответствующего свойства могло быть легко пересчитано на температуру, а измерения не зависели бы от природы этого тела.
В термодинамике уравнение, связывающее температуру с какими-либо другими свойствами (параметрами состояния) системы, называется уравнениям состояния системы, причём оно может быть получено не из термодинамического анализа, а по другим физическим соображениям (методами статистической механики) и (или) эмпирически. В настоящее время такое уравнение в точности известно только для идеального газа (уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева):
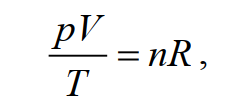 (5)
(5)
где T – температура, p – давление, V – объём, n – число молей, R – универсальная газовая постоянная, которая является фундаментальной константой и связана с другими константами соотношением:
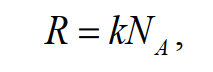 (6)
(6)
где k – постоянная Больцмана, NA – число Авогадро.
Это уравнение считается точным; границы его применимости обусловлены лишь границами корректности использования понятия «идеальный газ» для данной системы. Здесь температура может быть вычислена по другим параметрам состояния системы – p , V и n , которые базируются на других основных единицах СИ и могут быть легко измерены. Таким образом, система с идеальным газом может служить основой термометра, показания которого могут быть сразу переведены на температуру. Это лежит в основе первичной термометрии.
С другой стороны, в повседневной жизни известны другие термометры, которые широко и с лёгкостью используются. Ранее был упомянут стеклянный ртутный термометр. Выходным физическим параметром, который меняется с температурой, в нём служит длина столбика ртути в капилляре. Но эта длина непосредственно, с помощью каких-либо уравнений, не связана с температурой.
Другими примерами могут служить металлические термометры сопротивления и термопары, где выходными электрическими сигналами являются электрическое сопротивление и термо-э.д.с. соответственно. Эти параметры также не могут быть непосредственно связаны с температурой. Таким образом, во всех этих случаях, требуется градуировка по первичным термометрам, то есть экспериментальное определение соответствующих зависимостей. Все эти термометры являются вторичными и относятся ко вторичной термометрии.
В первичной термометрии используются термометры, показания которых сразу могут быть переведены в температуру, во вторичной – термометры, требующие градуировки по первичным.
В уравнениях, используемых для первичных термометров, не должно быть неизвестных параметров, зависящих от температуры. Так как точные уравнения состояния для конденсированных фаз неизвестны, использование их в качестве термометрических тел первичной термометрии невозможно. Что касается реальных газов, наиболее универсальным является уравнение состояния с вириальными коэффициентами:
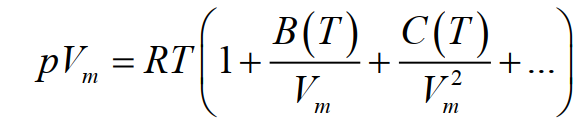 (7)
(7)
где Vm = V/n — мольный объём, B (T) и C (T) — второй и третий вириальные коэффициенты (первый вириальный коэффициент A равен единице). Ряд в скобках бесконечный сходящийся, что позволяет его ограничивать с обеспечением требуемой точности. Вириальные коэффициенты сами зависят от температуры и определяются экспериментально (в некоторых случаях могут быть рассчитаны).
Следует заметить, что при B (T) = 0 и C (T) = 0 уравнение (7) переходит в pVm = RT , то есть соответствует (5). Если в качестве термометрического тела выбрать конкретный реальный газ с быстро убывающим рядом в (7) и экспериментально определить вириальные коэффициенты, то такая система с некоторой точностью может использоваться в первичной термометрии. Это расширяет возможности соответствующих газовых термометров в плане диапазона температурных измерений.
Кроме газовых, в первичной термометрии используются акустические, шумовые термометры и термометры излучения, а также, с некоторыми оговорками, – магнитные термометры. Как правило, они очень сложны в устройстве и не применяются в промышленности и быту (за исключением термометров излучения).
Примерами вторичных термометров могут служить уже упоминавшиеся жидкостные (ртутные) термометры, термометры сопротивления и термопары, которые по сравнению с первичными весьма компактны, просты в использовании и иногда обладают большей чувствительностью. Они применяются в практике измерения температуры повсеместно, но требуют градуировки по первичным термометрам.
При использовании газовых термометров, как первичных, температура рассчитывается по уравнениям (5) или (7), при этом необходимо знать значение констант R или k , а давление и объём сравнительно легко измеряются, то есть определяются через другие основные единицы СИ. До недавнего времени k определяли экспериментально при значении тройной точки воды 273,16 К, которое считалось точным.
После принятия XXIV Генеральной конференцией по мерам и весам (2011 г.) решения о ревизии Международной системы единиц, значение постоянной Больцмана должно быть зафиксировано, после чего она будет считаться определённой точно, как k = 1,3806X ·10-23 Дж / К . Здесь Х заменяет одну или более значащих цифр, которые должны будут определены в дальнейшем на основании наиболее точных рекомендаций CODATA (Комитет по данным для науки и техники). Этот Комитет выпустил набор фундаментальных констант в 2018 году, уже основываясь на новой редакции СИ. В будущем возможно уточнение значения k , что может привести к корректировке температуры тройной точки воды и единицы температуры.
При экспериментальном же определении R или k (они пересчитываются друг в друга по (6), при этом число Авогадро NA устанавливается независимо) требуется измерить параметры состояния равновесной системы при температуре тройной точки воды. До последнего времени наиболее точные экспериментальные значения этих величин получались методом предельно разреженного газа по (5) и (7) при известной опорной температуре.
Другой метод определения R основан на измерении скорости звука в газе. Скорость звука c0 в идеальном газе при температуре T0 определяется выражением:
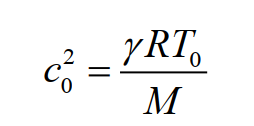 (8)
(8)
где γ – показатель адиабаты, то есть отношение теплоёмкостей газа при постоянном давлении cp и при постоянном объёме cV (эта величина может быть вычислена), T0 = 273,15 К , M – мольная масса.
Экспериментальные измерения скорости звука в реальном газе при разных давлениях позволяют найти c0 в пределе низких давлений.
Величина k может быть определена из полной энергии теплового излучения E (T0), испускаемого чёрным телом при температуре T0 по выражению (закон полного излучения Стефана-Больцмана):
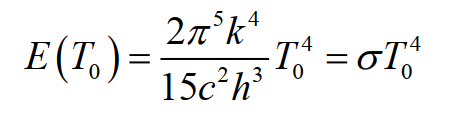 (9)
(9)
где c – скорость света, h – постоянная Планка, σ – постоянная Стефана–Больцмана. Измеряя E (T0) , можно получить значение σ, и, следовательно, k , поскольку величины c и h известны с более высокой точностью, чем это необходимо для определения k. В уравнение (9) был введён геометрический фактор, учитывающий невозможность экспериментального измерения излучения, испускаемое полусферой.
Ещё один метод определения k основан на измерении электрических шумов сопротивлений. Среднеквадратичное напряжение шумов V2 на сопротивлении Ω Ом равно:
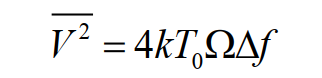 (10)
(10)
где Δf – ширина полосы. Затрудняют использование этого уравнения для определнения k сложности, связанные с достаточно точным измерением Δf.
Все эти методы служат основой для соответствующих первичных термометров, предоставляющих данные, независимые от газовой термометрии.
6. Очерк истории развития понятия температуры и температурных измерений
Как уже отмечалось, в силу того, что температура является величиной интенсивной, она требует совершенно иного подхода при её измерении по сравнению с другими величинами, такими как, например, масса или время. Развитие торговли ещё на заре цивилизации привело к появлению денег в виде монет из драгоценных металлов, стоимость которых оценивалось по массе; астрономические наблюдения в древних цивилизациях и даже в более ранние периоды установили первые календарные системы с точной периодизацией по времени.
Интуитивное понимание температуры, как меры нагретости тел, с оценкой «теплее – холоднее» возникло ещё на заре развития человечества. «Бытовая шкала температур», если можно так выразиться, отражала весьма приблизительные, субъективные понятия: «стужа, холод, прохлада, утренняя свежесть, норма, летнее тепло, жара. зной» и т.д. У древних металлургов уже были такие понятия, как «красное» и «белое каление» Живые организмы при температуре тела способны реагировать на изменения порядка 0,1 К.
Однако всё это не привело к появлению каких-то эталонов и шкал температур, пусть поначалу и несовершенных. Понимание температуры тесно связывалось с теплотой, и это вносило дополнительную путаницу. Уже в те времена было замечено, что тепло всегда переходит от горячего к холодному самопроизвольно и устанавливается равновесие при состоянии, более холодном, чем первоначальное горячее, и при более горячем, чем первоначальное холодное, но это не связывалось с каким-то определённым свойством тел (с тем, что впоследствии назовут «температурой»).
В Древнем мире с появлением науки возникают термины, близкие к понятиям «теплоты» и «температуры». Во многих философских системах фигурировали понятия «элементарного огня» (например, Демокрит и Левкипп), в «четырёхэлементном мире» наряду с землёй, водой и воздухом был «огонь» (Аристотель и более древние авторы). В медицине также использовалось понятие «элементарный огонь» (Гиппократ); у больных часто наблюдался «жар». Но какие-либо измерения величин, связанных с температурой, опять-таки не проводились и никакие шкалы не строились.
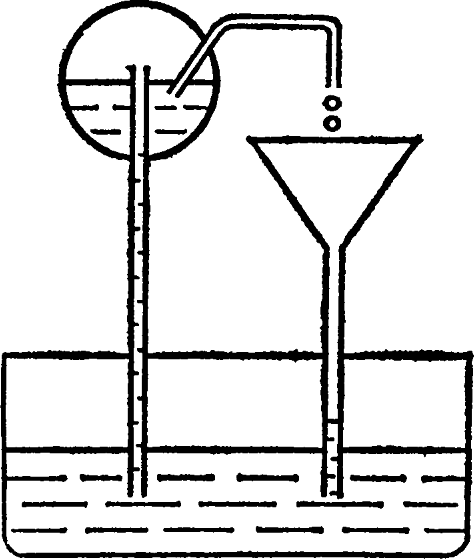
Рис. 10. Термоскоп Герона Александрийского
Герон Александрийский (III – II век до н. э. или I век н. э.). зная о свойстве воздуха расширяться при нагревании, описал прибор для наблюдения этого (рис. 10). Шаровой сосуд, наполненный водой и воздухом, выставляется под лучи солнца. Воздух расширяется и вытесняет воду из сосуда. Вода попадает в резервуар и после охлаждения вновь поднимается по вертикальной трубке в сосуд. Таким образом, вытеснение воды означает нагревание. Похожий прибор был создан также Филоном Византийским (280 до н. э – 220 до н. э), но все эти приборы не предназначались для измерения температуры непосредственно.
В медицинских трактатах Галена (римлянин греческого происхождения, 130 – 217 н. э.) описано подобие клинической термометрии, основанной на идеях Аристотеля. Полагалось, что люди различаются по пропорциям теплоты, холода, влажности и сухости. Он предложил эталон «нейтральной» температуры, для которого использовалась смесь из равных частей кипящей воды и льда, причём каждому из этих компонентов он приписывал четыре градуса тепла и четыре градуса холода соответственно. До нас не дошло никаких сведений о способах применения такого эталона. (Этим методом можно было получить температуру около 10°C ).
В 1578 г. врач Хаслер Бернский в своём труде De logistica medica, следуя Галену, приписывал своим лекарственным смесям различные градусы тепла и холода. Для составления своих рецептов он использовал температурную шкалу, содержащую, по Галену, четыре градуса тепла, четыре градуса холода и нуль между ними. Он ввёл также шкалу широт, предположив, что жители экваториальных областей имеют четыре градуса тепла, а жители полярных районов – четыре градуса холода. Согласно этим шкалам, вычислялись смеси лекарств в зависимости от места жительства пациента (!).
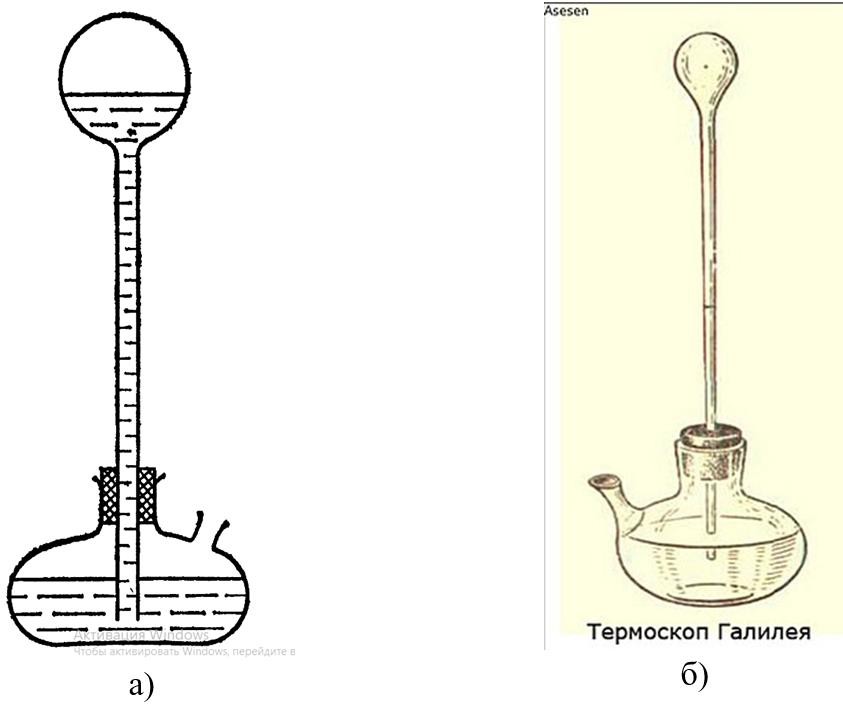
Рис. 11. Термоскоп Галилея: а) – схема, б) – изображение.
Физиолог Санторио Падуанский опубликовал, как считается, первое описание прибора, именно определяющего температуру, в 1612 году в «Комментариях на Галена» (Commentaries on Galen).
Честь изобретения воздушного термометра приписывается Галилею (примерно в 1592 г.). В его термоскопе (рис. 11) по высоте водяного столба можно судить о том, является температура высокой или низкой. О применении такого прибора на практике упоминается в 1611 и 1613 гг.
Прибор состоял из стеклянного баллончика, заполненного воздухом и сообщающегося тонкой трубкой с сосудом, в котором находилась закрашенная жидкость (вода или спирт). изменение температуры воздуха в баллончике сопровождалось изменением уровня закрашенной жидкости в трубке. (Первоначально баллончик нагревался, и трубка опускалась в сосуд с жидкостью; после остывания жидкость поднималась по трубке).
Существенным недостатком этого первого из известных термометров являлась чувствительность к изменению атмосферного давления. В 1626 г. Галилей вместе с Санторио Падуанским создал первый ртутный термометр.
Галилею также приписывается создание так называемого «термометра Галилея» (точных сведений о создателе нет). Он представляет собой вертикально расположенный стеклянный цилиндр, почти до верха заполненный водой (или другой жидкостью) и запаянный сверху (рис. 12, а). Внутри, в жидкости, помещены несколько запаянных стеклянных буйков шарообразной формы, наполовину заполненных подкрашенной жидкостью различных цветов. Снизу буйков прикреплены небольшие металлические бирки с обозначением на них соответствующей температуры (рис. 12, б).
С повышением температуры плотность воды уменьшается и буйки могут тонуть, если отношение их массы к объёму становится больше плотности воды (и наоборот) – принцип показан на рис. 13. Массы буйков подобраны таким образом, чтобы соответствовать дискретным значениям температур с шагом, например, 1 К в диапазоне, как правило, 16 ÷ 28°C (комнатные температуры). В XVII в., разумеется, буйки маркировались в других единицах, по-видимому, – каких-то условных. Температура определялась по всплывшему буйку с наименьшей температурной маркировкой.

Рис. 12. Термометр Галилея: а) – общий вид, б) – стеклянные буйки с бирками.
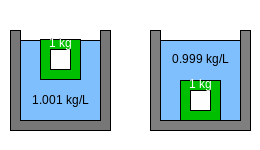
Рис. 13. Принцип действия термометра Галилея
В настоящее время такой термометр имеет только декоративное значение.
Однако первый жидкостной термометр, в современном понимании, был создан французским врачом Жаном Рэ (Jean Rey) в 1632 г., – с открытым концом и водой в качестве термометрической жидкости. Этот прибор усовершенствовал в 1641 г. великий герцог Тосканский Фердинандо II Медичи, покровитель и ученик Галилея, создав вертикальный стеклянный запаянный термометр со спиртом в качестве жидкости.
Трубки этих термометров имели, несколько десятков «градусных» меток, нанесённых стекловидной эмалью непосредственно на трубки. что представляло собой равномерную шкалу, которая, однако, не была привязана к каким-то реперным точкам, и «градус» был весьма условным понятием. Сохранились сведения о том, что один из таких термометров в снегопад показывал 20 «градусов», а в знойный день – 80 «градусов».
В 1654 году было изготовлено несколько «50-градусных» термометров, которые были отправлены из Флоренции (Тоскана) во многие города Италии, где были оценены очень высоко. Флорентийское стеклодувное искусство того времени было весьма развито (некоторые достижения не превзойдены до сих пор, а многие секреты утеряны). Это позволило получить несколько термометров с согласованными между собой показаниями, очень чувствительными и, самое главное, стабильными.
Тогда же флорентийские стеклодувы создали термометр, необыкновенно длинный капилляр которого был закручен в 12 витков. а деления шкалы представляли собой горизонтальные стеклянные брусочки, которые были припаяны к капилляру и придавали ему жёсткость. Прибор был очень чувствителен (реагировал на дыхание) и стабилен в показаниях. В 1657 г. проводились опыты со ртутью в качестве термометрической жидкости, но, к сожалению, такие термометры сочли менее удобными.
Можно считать, что метрологическую основу термометрии заложил уже упоминавшийся падуанский врач Санторио. На одном из термоскопов Галилея, который по факту стал образцовым, он нанёс две абсолютные отметки и регламентировал систему поверки по этому термоскопу для всех флорентийских термометров. Значения фиксированных точек не сохранились, однако известно, что точка таяния льда соответствовала 13,5 градусам флорентийской шкалы.
В 1661 г. флорентийский спиртовой термометр был привезён в Англию, где Роберт Гук усовершенствовал его (1664 г.), предложив подкрашивать спирт в красный цвет, изобрёл устройство для нанесения шкалы и усовершенствовал технологию производства, перейдя от изготовления термометров совершенно одинаковых размеров к приборам, основанным на равных приращениях объёмов жидкости с ростом температуры. Последнее позволило снизить требования к мастерству стеклодувов и повысило точность измерений. Гук не избежал и ошибок, пытаясь основывать измерения на точке замерзания воды и полагая, что температура начала замерзания ванны с водой и полного замерзания воды различны (видимо сказалось изменение плотности воды при 4°C). Тем не менее были изготовлены эталонные термометры (эталон Грешем Колледжа), по которым градуировались другие термометры (1665 г.). Приборы эти использовались вплоть до 1709 г.
Французский академик Гийом Амонтон в 1702 году впервые разработал газовый термометр постоянного объёма. Термометрическим веществом служил воздух. Этот термометр представлял собой U-образную стеклянную трубку, левое колено которой имело риску и подходило к замкнутому сосуду с воздухом, а в правое колено, более длинное, заливалась ртуть, которая переходила в левое колено до риски. Таким образом, объём воздуха в левой части прибора фиксировался; при изменении температуры воздух расширялся или сжимался и уровень ртути соответственно понижался или повышался. Добавляя или убавляя ртуть в правом колене, можно было подогнать её уровень к риске; температура определялась по высоте столба ртути в правом колене относительно риски на левом колене.
Приняв обычную температуру (видимо, близкую к комнатной) за исходную, Амонтон провёл измерения зимой и летом и определил, что отношение «самого большого летнего тепла» к «самому большому летнему холоду» в Париже составляет примерно 6:5. На основании этих измерений он впервые предположил, что самая низкая возможная температура должна соответствовать наименьшему из возможных (или стремящемуся к нулю) давлению газа в данном объёме.
Полагая, что теплота является одной из форм движения, Амонтон пришёл к выводу, что при этом должно прекратиться всякое движение частиц (1703 г.), а такую минимальную температуру логично принять за нуль. В теоретическом плане это являлось большим прорывом в понимании температуры, так как фактически было введено понятие абсолютного нуля температур. На этом принципе впоследствии основывался Кельвин, разработавший абсолютную шкалу температур с использованием абсолютного нуля как одной их двух реперных точек. Амонтон впервые предпринял попытку определить положение абсолютного нуля относительно точки таяния льда и получил значение температуры, в пересчёте на современную шкалу, -239,8°C , что является неплохим результатом с учётом тогдашнего развития измерительной техники.
Таким образом, был заложен один из краеугольных камней научного понимания температуры. Другим кардинальным направлением развития термометрии явилось создание температурных шкал.
1. Самой первой температурной шкалой с фиксированным нулём считается шкала Гука. Её предложил в 1662 году английский естествоиспытатель и изобретатель Роберт Гук (Хук).
Как уже отмечалось выше, Гук разработал свою шкалу на основе попавшего к нему в 1661 термометра из Флоренции и уже через год описал её в работе «Микрография». Ранее (около 1660 года; по другим сведениям – в 1665 году), он вместе с Христианом Гюйгенсом предложил в качестве опорных точек для температурной шкалы температуры замерзания и кипения воды, установив экспериментально их постоянство (в дальнейшем это некоторое время подвергалось сомнению и уточнялось).
К подобным выводам Гуку помогла прийти приверженность молекулярно-кинетическим воззрениям (в отсутствие в то время законченной теории), так как он считал причиной передачи теплоты механическое движение частиц вещества.
Гук определил один градус (градус Гука ºH ) как изменение объёма спирта в термометре на 1/500 часть (это примерно равнялось 2, 4 °C). Как уже говорилось, с 1663 года по решению Лондонского Королевского общества по развитию знаний о природе термометр Гука использовался в качестве стандартного, по нему градуировались другие термометры.
С помощью этого термометра были проведены первые более-менее надёжные метеорологические измерения. Так наибольшая летняя жара была зафиксирована в 13°H ( 31°C ), а наибольший холод зимой как -7°H ( -17°C ).
Формула для перевода градусов Гука в градусы Цельсия и обратно:
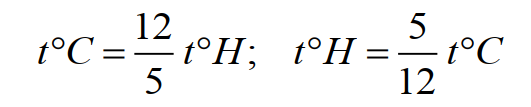 (11)
(11)
2. Одну из первых научно обоснованных шкал предложил Исаак Ньютон в 1701 году (градус Ньютона ºN ) для обеспечения теплофизических исследований, которыми он занимался (термометрическая жидкость – льняное масло). В этой шкале нулю соответствовала точка замерзания пресной воды, температуре человеческого тела было приписано 12 градусов (дюжина – распространённое число), а температура кипения воды получилась довольно точно равной 33 градусам. Формулы перевода градусов Ньютона в градусы Цельсия и обратно:
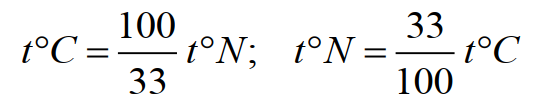 (12)
(12)
3. В том же 1701 году датским астрономом Оле Кристенсеном Рёмером была предложена шкала (градус Рёмера °Rø ), ставшая прообразом знаменитой шкалы Фаренгейта, который посещал Рёмера в 1708 году. С целью расширения шкалы влево Рёмер взял за нуль температуру замерзания солёной воды (примерно на 14 кельвинов меньше воды пресной в соответствии с криоскопическим эффектом).
Основная часть шкалы простиралась до температуры кипения воды, которой было присвоено значение 60 градусов (распространённое число в астрономических расчётах). Температуре человеческого тела приписывалось значение 30 градусов, причём это считалось второй реперной точкой наряду с нулём шкалы. Пересчёт этого значения на шкалу Цельсия даёт 42 °С , то есть измерения Рёмера были не совсем точны. Температура пресной воды соответствовала 7,5 °Rø .
Формула для перевода градусов Рёмера в градусы Цельсия и обратно:
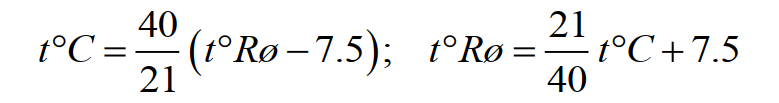 (13)
(13)
4. Габриель Фаренгейт, немец по национальности, работавший в Голландии и Англии, впервые наладил серийное производство термометров, изготовление которых было унифицировано и показания имели высокую воспроизводимость. Он в 1724 разработал шкалу температур (градус Фаренгейта °F ), которая применяется в США и некоторых других странах до сих пор. При разработке этой шкалы Фаренгейт работал со спиртовыми термометрами, но в дальнейшем впервые на постоянной основе использовал ртуть в качестве термометрического тела.
В предложенной шкале в качестве нуля была выбрана наиболее низкая из имеющихся в лабораторной практике температура, которая получалась в смеси вода – лёд с нашатырём (примерно -17,8°С ). Вторая точка соответствовала температуре «человеческой крови» (или человеческого тела); эта температура была предложена ещё Ньютоном (по шкале Цельсия – 35,55°С ; по современным данным температура тела человека равна 36,6°С ).
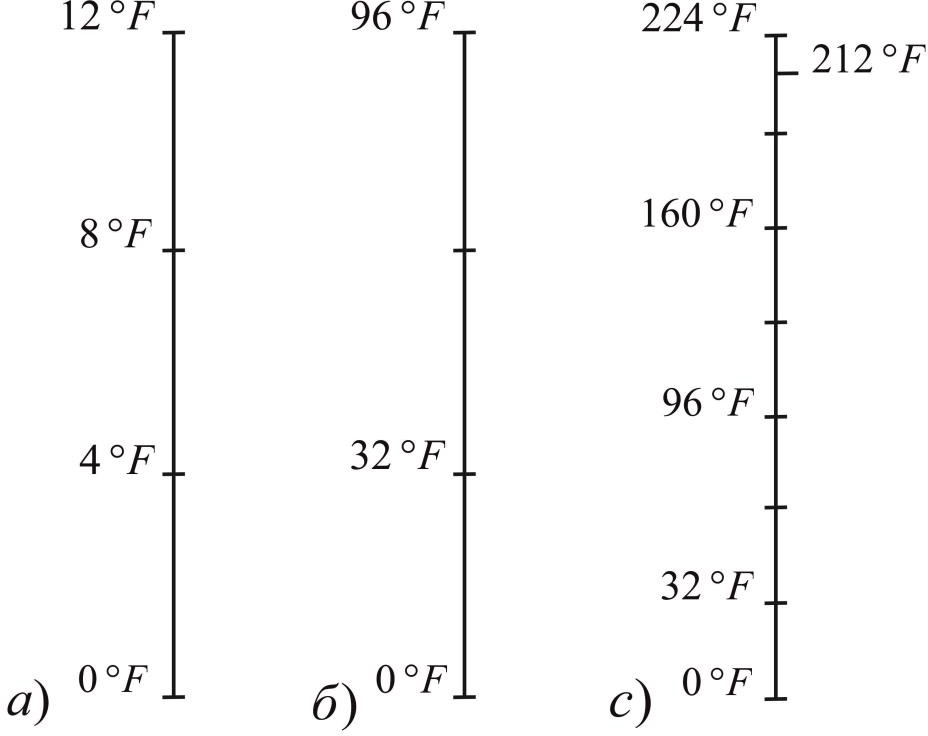
Рис. 14. Шкала температур Фаренгейта. а) Первоначальный вариант. б) Окончательный вариант: 0 °F = -17,8°С , температура «человеческой крови» 96°F , таяния льда 32°F . в) Расширенная шкала Фаренгейта для ртутных термометров: точки кипения воды 212°F ;.
Промежуток разделялся на 12 градусов (дюжина), и, таким образом, получался градус Фаренгейта (рис. 14-а). Температуры выше точки 12 градусов фиксировались уже с использованием этой единицы температуры; так была получена, например, точка кипения воды. Температура таяния льда по первичной шкале составила 4 градуса, то есть довольно точно составляла треть от шкалы.

Рис. 15. Сравнение шкал ртутного и спиртового термометров.
Такая первичная шкала давала возможность только грубой оценки температуры. В дальнейшем Фаренгейт трижды последовательно делил градусы пополам, что привело к восьмикратному уменьшению единицы и позволило проводить более точные измерения. В окончательном варианте температура «человеческой крови» составляла 96°F , а таяния льда – 32°F (рис. 14-б).
Необходимость более точного измерения температуры обусловил переход к использованию ртутных термометров (рис. 14в, 15). Это позволило, в частности, расширить первоначальный диапазон температур (при сохранении единицы градус Фаренгейта) далеко вверх, до точки кипения воды 212°F ; в дальнейшем были измерены температуры кипения жидкостей вплоть до 600 градусов. Исследования Фаренгейта дали обоснование надёжности выбора тех или иных реперных точек.
Температура замерзания воды должна была быть перепроверена по причине возможного переохлаждения жидкости. Это явление замерзания при более низкой, чем точка плавления, температуре, в те времена наблюдалось для многих других жидкостей. Причиной этого было слишком медленное охлаждение при дефиците центров кристаллизации. Фаренгейт установил, что высокостабильной являлась смесь льда с водой, а не постепенное замерзание воды при отсутствии перемешивания. Также он установил, что температура кипения воды зависит от атмосферного давления. В 1736 году точки замерзания и кипения воды при фиксированном барометрическом давлении были приняты в качестве реперных.
Шкалы Цельсия и Фаренгейта пересекаются в одной точке: -40°F = -40°C . Абсолютному нулю температур по шкале Фаренгейта соответствует значение -459,67°F .
Формула для перевода градусов Фаренгейта в градусы Цельсия и обратно:
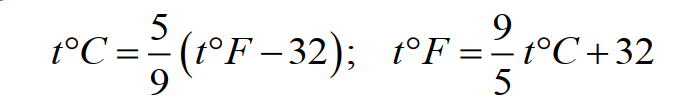 (14)
(14)
5. Французский зоолог и физик Рене Антуан Фершо де Реомюр в 1730 году разработал шкалу, принципиально отличающуюся от шкалы Фаренгейта, на основе спиртового термометра (градус Реомюра °R или °Ré). В настоящее время ошибочно считается, что основная часть его шкалы простирается от точки плавления льда ( 0°R = 0°С ) до точки кипения воды, и этот диапазон разбит на 80 градусов (80°R =100°С ), что напоминает известную шкалу Цельсия. Однако оригинальная шкала Реомюра строилась на других принципах и первоначально градус Реомюра почти равнялся градусу Цельсия и имело место равенство 80°R ≈ 78°С .
Изучив работы Фаренгейта, Реомюр обратил внимание на слишком произвольный выбор реперных точек – температуры замерзания смеси воды, льда и нашатыря, и температуры человеческого тела. Это вносило, по его мнению, слишком большие исходные погрешности, поэтому он считал необходимым использовать более простые системы, такие как температура замерзания и кипения индивидуального вещества – воды. В те времена уже было установлено постоянство температуры замерзания воды (или таяния льда), но считалось, что температура кипения воды может быть заметно разной, даже при каком-то постоянном давлении. Это в своё время и способствовало появлению шкалы Фаренгейта.
Реомюр перед академической комиссией продемонстрировал эксперименты, опровергающие эти заблуждения. Однако из перечисленных двух Реомюр выбрал для своей шкалы только одну точку – температуру замерзания воды. В качестве термометрического тела он выбрал этиловый спирт, который, в отличие от воды, мало растворяет газы. Ртуть, по каким-то причинам, он первоначально не стал использовать.
Верхний предел такого термометра ограничивался температурой кипения спирта ≈ 78°С . В те времена не умели получать 100%-ный спирт, так как он образует с водой азеотропную смесь при 95,6% спирта по массе и остальную воду невозможно удалить перегонкой. По современным данным азеотропная смесь (спирт-ректификат) имеет температуру кипения 78,15°С , а абсолютный спирт (практически 100%-ный) – 78,39°С . Жидкость, использованная Реомюром, как он сам отмечал, содержала не более 5% воды и была очищена от растворенных газов. Термометр представлял собой тонкую стеклянную трубку, припаянную к круглой колбочке со спиртом; сверху трубка герметизировалась замазкой. Это устройство напоминает современные жидкостные термометры.
Реомюр установил, что при нагревании от температуры таяния льда до температуры кипения спирта ( ≈ 78 °С ) последний расширяется приблизительно на 8% (расчётное значение – 8,45%, так как коэффициент объёмного термического расширения спирта 0, 001081 К -1 ).
Температуру кипения спирта Реомюр не стал брать в качестве второй реперной точки, как ненадёжную, а задал в качестве основы для построения шкалы фиксированное значение градуса Реомюра ( °R ), как величину расширения спирта на 8‰ (промилле, тысячная доля величины) по объёму. В диапазоне 0°С ÷ 78°С таких градусов укладывалось 80, так и возникла 80-градусная шкала Реомюра. Однако при производстве конкретных термометров такой принцип построения шкалы оказался крайне неудобным, что и привело впоследствии к ошибочному переосмыслению градуса Реомюра. Кроме того, недостатками шкалы являлись её неравномерность (спирт) и ограниченность температурой кипения спирта.
Позднее термометрическая жидкость была заменена на ртуть при сохранении определения градуса Реомюра. Ещё при жизни учёного были проведены измерения точки кипения воды в градусах его шкалы (ранее со спиртовыми термометрами это было невозможно). Вначале было получено значение 85°R (Жан Тийе и Жан-Антуан Нолле).
Все последующие измерения дали величины от 100°R до 110°R . По современным данным, должно было получиться значение 108,1°R. В 1772 г. во Франции в качестве стандартной была принята температура кипения воды, равная 110°R , и это действовало до 1794 г. В дальнейшем, во второй половине XVIII века, термометры Реомюра изготавливались во Франции повсеместно, причём спирт был заменён ртутью. Параллельно появились термометры со 100-градусной шкалой Цельсия.
Ремесленникам было сложно выдерживать истинный градус Реомюра на своих приборах (по расширению спирта в промилле от объёма), гораздо проще было изготавливать термометры по двум реперным точкам с делением диапазона на градусы, как в случае термометров со шкалой Цельсия.
Постепенно заказанные термометры со шкалой Реомюра стали изготавливать по упрощённой технологии, деля диапазон из двух реперных точек на 80 градусов. При этом ошибочно за верхний диапазон принималась точка кипения не спирта, с которым уже практически не работали, а воды, которая хорошо воспроизводилась ртутными термометрами. К концу XVIII века шкала Реомюра была переопределена таким образом окончательно и в таком виде дожила до середины XX века. В настоящее время она практически не используется.
Формула для перевода градусов Реомюра в градусы Цельсия и обратно (по современным представлениям):
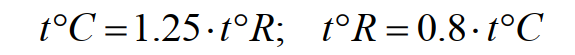 (15)
(15)
(по оригинальной шкале 1°R = 0,925 °C ).
6. В 1732 году французский астроном и картограф ЖозефНикола Делиль (Де Л’Иль), с 1725 до 1747 года служивший по приглашению в Петербургской Академии наук (первый академик астрономии), создал термометр, использующий ртуть в качестве рабочей жидкости (градус Делиля °D ).
Принцип построения шкалы был такой же, как у шкалы Реомюра — по изменению объёма термометрической жидкости. В качестве нуля была выбрана точка кипения воды, градуировка начиналась с этой температуры и производилась при охлаждении. При этом объём ртути уменьшался и за один градус было принято уменьшение на одну стотысячную. То есть шкала Делиля была «перевёрнутой», причём температурные отметки ниже точки кипения воды были положительными, а выше – отрицательными. С температурой таяния льда совпало значение 2400°D.
«Перевёрнутость» шкалы обычно объясняется бóльшим удобством градуировки. Шкала оказалась слишком мелкой при использовании и уже зимой 1738 года коллега Делиля по Петербургской академии, медик Иосия Вейтбрехт, уменьшил число градусов в диапазоне от точки кипения до точки замерзания воды в 16 раз и получил 150-градусную шкалу. Таким образом по факту шкала Делиля стала основываться на двух реперных точках.
Эта шкала была широко распространена в России и использовалась около ста лет, особенно в течение XVIII века. В том числе – в Петербургской академии наук, в частности, Ломоносовым s41, который использовал термометры с общепринятым ныне направлением шкалы, поменяв местами значения 150°D и 0°D в опорных точках.
Формула для перевода градусов Делиля в градусы Цельсия и обратно:
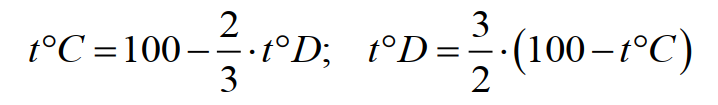 (16)
(16)
7. Наиболее удачная температурная шкала была предложена в 1742 году Андерсом Цельсием, шведским астрономом, геологом и метеорологом. Она широко применяется до сих пор во всех странах, кроме США (и четырёх небольших стран), несмотря на принятие в системе СИ шкалы Кельвина. Вначале она называлась просто стоградусной шкалой, и лишь позднее ей было присвоено имя Цельсия (градус Цельсия °C ).
Первым это предложил шведский химик Йёнс Якоб Берцелиус s43, а до этого в XVIII веке соответствующий термометр назывался «шведским», а в самой Швеции – термометром Штрёмера. Официально наименование «градус Цельсия» было принято лишь на IX Генеральной конференции по мерам и весам в 1948 году.
![]()
Рис. 16. Рисунок термометра, сделанный самим Цельсием, из статьи Observationer om twänne beständiga grader på en thermometer, 1742.
Считается, что ещё в 1665 году голландский физик Христиан Гюйгенс и английский физик Роберт Гук рассматривали возможность использования в качестве отсчётных точек температурной шкалы точки замерзания и кипения воды. Цельсий на основе этой идеи разработал новую температурную шкалу, в которой точке кипения воды было присвоено значение 0 градусов, а точке плавления льда – 100 градусов (рис. 16).
Такая «перевёрнутость» шкалы, как и в случае шкалы Делиля, скорее всего объясняется бóльшим удобством при градуировке термометров, так как при охлаждении системы изменение температуры происходит более плавно и стабильно, чем при нагревании. Однако на практике использовать такие термометры не очень удобно, поэтому уже после смерти Цельсия, его современники и соотечественники ботаник Карл Линней (1745 год) и астроном Мортен Штрёмер перевернули эту шкалу и использовали её в общепринятом ныне виде (сведения об этом противоречивы, возможно, сам Цельсий перевернул свою шкалу по совету Штрёмера).
Таким образом, 0°C стала соответствовать таяния льда, а 100°C – температура кипения воды.
Цельсий разработал свою шкалу на основе полученного им большого экспериментального материала (он представлен в работе «Наблюдения двух фиксированных положений на термометре»). Им было доказано, что температура таяния льда не зависит от внешнего давления, и это позволило правильно определить набор требований, позволяющих достаточно точно воспроизводить эту реперную точку. Также он очень точно измерил температуру кипения воды в зависимости от атмосферного давления, и не только подтвердил наличие такой зависимости, но и разработал научную методику расчётов калибровки опорной точки 100°C термометров в зависимости от барометрического давления и положения над уровнем моря.
Шкала Цельсия считается линейной в основном интервале от 0°C до 100°C; линейность также предполагается и за границами этого интервала. Это является общим недостатком всех эмпирических систем термометрии, так как шкалы любых жидкостных термометров неравномерны. Это явно имеет место в случае спиртовых термометров, для ртутных – в гораздо меньшей степени; с какой-то точностью шкалы последних можно считать равномерными, но при прецизионных измерениях неравномерность ртутной шкалы даёт о себе знать.
Понятие «градус Цельсия» настолько широко вошло в практику измерения температур, как на бытовом уровне, так и в технике, науке и производстве, что Международная система единиц (СИ) допускает его использование наряду с основной единицей температуры «кельвин». Градус Цельсия является производной единицей и, в настоящее время, считается равным кельвину (это справедливо лишь с некоторой точностью); соотношение между шкалами Кельвина и Цельсия (опять-таки в настоящее время) определяется по формуле:
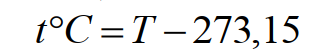 (17)
(17)
где T – температура в кельвинах. При использовании шкалы Цельсия обязательно выражение «градус Цельсия», как «единицы температуры Цельсия». Это закреплено в основных международных и российских документах: в Брошюре СИ, опубликованной Международным бюро мер и весов (МБМВ) и содержащей полное официальное описание СИ вместе с её толкованием, в ГОСТ 8.417-2002 «Единицы физических величин» и в «Положении о единицах величин, допускаемых к применению в Российской Федерации», утверждённом Правительством РФ.
8. Шкала Ламберта (градус Ламберта, специального обозначения не имеет), теоретически была предложена около 1760 года немецким физиком, оптиком, философом, математиком и астрономом Иоганном Генрихом Ламбертом. Шкала была абсолютной, где первая реперная точка соответствовала абсолютному нулю температур. Ламберт установил, что для построения шкалы будет достаточно ещё только одной опорной точки. Таковой была выбрана температура таяния льда и ей было приписано значение 1000 градусов. Температура кипения воды при этом получалась равной 1370 (по более точному расчёту – 1366,1) градусов. Принципы построения шкалы были очень прогрессивными для своего времени, но, к сожалению, практического применения шкала Ламберта не получила.
Формула для перевода градусов Ламберта в градусы Цельсия и обратно:
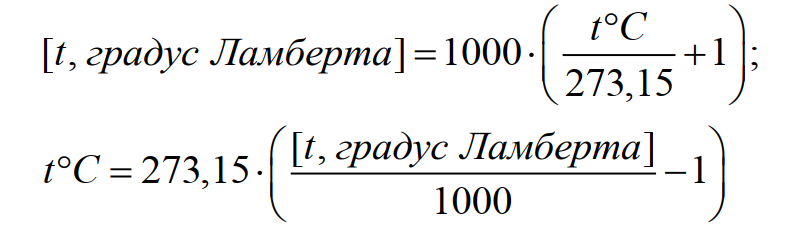 (18)
(18)
9. Ртутные термометры не позволяют измерять температуры выше точки кипения ртути ( 356°C ). Однако в технике и промышленности в целом даже в те времена требовалось измерять более высокие температуры (металлургия, стекольное и керамическое производство и т. д.). В XVIII веке (примерно в 1782 году) знаменитый английский художник-керамист и дизайнером Джозайя Уэджвуд предложил пригодный для этих целей метод измерения и связанную с ним шкалу.
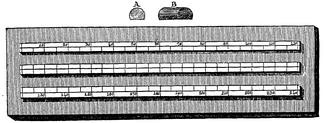
Рис. 17. Глиняный пирометр Уэджвуда.
Измерение температуры в печах по шкале Уэджвуда основано на определении величины усадки глины при нагревании, путём сравнения длины нагретых и холодных глиняных цилиндров. В 1782 году Уэджвуд соорудил устройство (по факту – пирометр, рис. 17), которое представляло собой два глиняных цилиндра с металлическими пластинами, наклонёнными под небольшим углом, со шкалой, разделённой на 240 частей.
Один из цилиндров не нагревался, и его длина соответствовала исходной температуре. Второй глиняный цилиндр после отжига сжимался и по степени его сжатия можно было судить о температуре в печи. Ноль по шкале Уэджвуда соответствовал 580,8°C («температура красного каления»), от него шкала была градуирована вниз на 240 градусов до отметки 54°C (соответствует «круглому» значению по шкале Фаренгейта 130°F ) и вверх до самых высоких температур.
Вначале метод и устройства Уэджвуда получили широкое распространение, но впоследствии были признаны неточными и вышли из употребления. Их несовершенство вызывало критику даже со стороны многих его современников, в частности, российского академика Я. Д. Захарова (конец XVIII – начало XIX века), который писал, что этим методом нельзя определить практически ни одну из температур («степень жара»).
Захаров выделил несколько основных недостатков пирометров Уэджвуда:
- а) зависимость сжимаемости глины от её сорта;
- б) малая чувствительность метода;
- в) деформация образца вплоть до его разрушения;
- г) неточность в определении нулевых точек.
Уэджвуд пытался сравнить свою шкалу с другими шкалами, использовал для этого серебряные образцы, определял температуры плавления некоторых металлов, но эти измерения оказались крайне неточными, значения расходились с реальными в несколько раз.
«Французский химик Луи Гитон де Морво (1737—1816), используя свой пирометр, протестировал шкалу Уэджвуда и пришёл к выводу, что её нулевая отметка должна быть значительно ниже — примерно 269 °C, а не 580,8 °C; а низшая точка располагаться на уровне 16,9 °C, а не 54 °C. Тем не менее даже после этого Уэджвуд не отказывался от своих представлений о точках плавления металлов. После изобретения точных пирометров, например, пирометра Джона Даниэля в 1830 году, шкала Уэджвуда окончательно вышла из употребления».
Формула для перевода градусов Уэджвуда в градусы Цельсия и обратно (для основной части шкалы от 54°C до 580,8°C ; поскольку шкала Уэджвуда очень неточна, перевод практического значения не имеет):
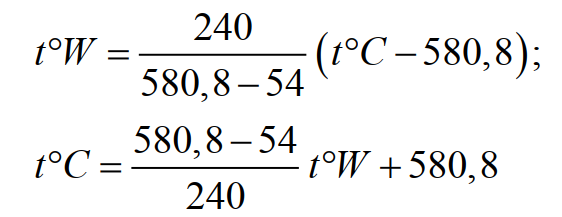 (19)
(19)
10. Разработанные ранее температурные шкалы вполне удовлетворительно работали в основном диапазоне температур, то есть, – между двумя реперными точками. Однако за пределами этого интервала, особенно при повышенных температурах, погрешности измерений сильно возрастали. Как уже отмечалось, это является недостатком всех систем, основанных на эмпирической температуре. Чтобы снизить ошибку равномерных шкал из-за неравномерного расширения термометрической жидкости, английский физик, химик, метеоролог и естествоиспытатель Джон Дальтон (Дэлтон) примерно в самом начале XIX века разработал логарифмическую шкалу для проведения измерений при высоких температурах (градус Дальтона °Da ).
Поскольку шкала логарифмическая, градус Дальтона не имеет определённого числового значения, но температура может быть пересчитана на другие шкалы по формулам. Нуль шкалы Дальтона соответствует нулю Цельсия ( 0°Da = 0°C ); отрицательные температуры по Цельсию соответствуют отрицательным температурам по Дальтону, положительные – положительным, но имеют другие числовые значения. Абсолютный нуль температур равен -∞ °Da , тоесть шкала отражает его недостижимость.
Формула для перевода градусов Дальтона в градусы Цельсия и обратно:
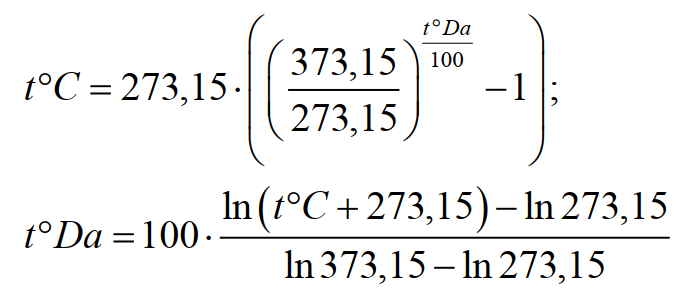 (20)
(20)
(Примечание. Обычно во второй формуле приводится десятичный логарифм lg , а не натуральный ln , но такая замена оправдана, так как эти логарифмы отличаются постоянным множителем ln x ≈ 2,3·lg x ).
11. Абсолютная термодинамическая шкала температур была предложена в 1848 году британским физиком, механиком и инженером Уильямом Томсоном, лордом Кельвином Ларгским из Айршира. Соответствующая единица термодинамической температуры в Международной системе единиц (СИ) кельвин K , – одна из семи основных единиц СИ, – была названа в его честь. До 1968 года кельвин официально именовался градусом Кельвина ( °K ).
В 1848 году Томсон, будущий лорд Кельвин, в своей работе «Об абсолютной термометрической шкале» («On an Absolute Thermometric Scale») обосновывает необходимость температурной шкалы, одна из реперных точек которой (нулевая) будет соответствовать абсолютному нулю температур («предельной степени холода» по тогдашней терминологии), а ценой деления будет градус Цельсия, наиболее широко применяемая к тому времени единица. Значение абсолютного нуля, -273,15°C было получено как обратное от 0,003661 — коэффициента объёмного расширения идеального газа на градус Цельсия; а эта величина была измерена экспериментально. Фактически второй реперной точкой служила температура замерзания воды ( 0°C или 273,15 K ). В то время шкала не была принята официально, хотя резонность такого подхода признавалась.
Недостатком первоначальной трактовки абсолютной шкалы являлось привязка к ней единицы эмпирической температуры (градус Цельсия), который определялся в фактически неравномерной шкале. Поэтому единица температуры должна была быть переопределена. Лишь в 1954 году, более чем через 100 лет после предложения Кельвина, Третья резолюция Х Генеральной конференции по мерам и весам (ГКМВ) дала шкале Кельвина современное определение, взяв температуру тройной точки воды в качестве второй опорной точки и приняв, что её значение составляет ровно 273,16 кельвина (тогда ещё – «градуса Кельвина»).
Напомним, что разница между тройной точкой воды и точкой замерзания воды составляет 0,01K (или 0,01°C ). Температура тройной точки воды была выбрана вместо точки замерзания, как более стабильная и точнее воспроизводимая. В 1967/1968 годах Третья резолюция XIII Генеральной конференции по мерам и весам единица термодинамической температуры была переименована в «кельвин» и переопределена более явно, как 1/273,16 тройной точки воды.
Но даже после такой регламентации прецизионные измерения температуры могли зависеть от чистоты и изотопного состава самой воды. С целью сведения к минимуму этого влияния в 2005 году Консультативный комитет по термометрии установил для Международной температурной шкалы МТШ‑90 требования к изотопному составу воды при реализации температуры тройной точки воды.
Но наиболее кардинальным выходом стала резолюция XXVI Генеральной конференции по мерам и весам (2018 год) о будущей ревизии Международной системы единиц с переопределением кельвина через значение постоянной Больцмана, которая равна 1,380649 ·10-23 Дж / K , то есть – фундаментальной константы (предварительно это было решено на XXIV ГКМВ в 2011 году и подтверждено XXV ГКМВ, состоявшейся в 2014 году). Значение постоянной Больцмана будет зафиксировано, то есть будет считаться определённым точно (в дальнейшем, с развитием научных данных, это значение может быть скорректировано). При этом температура тройной точки воды останется равной 273,16 К, но её значение приобретёт погрешность и в дальнейшем будет определяться экспериментально.
В 2019 году предложенные изменения определений основных единиц Международной системы единиц (СИ), в том числе кельвина, вступили в силу. Теперь основные единицы СИ стали определяться через фиксированные значения фундаментальных физических постоянных. При этом величины всех единиц остались неизменными, однако из их определений окончательно исчезла привязка к материальным эталонам.
12. Шкалу Рэнкина предложил в 1859 году шотландский инженер, физик и механик, один из создателей технической термодинамики, Уильям Джон Макуорн Рэнкин . Эта шкала (градус Рэнкина °Ra ), также, как и шкала Кельвина, является абсолютной или термодинамической, то есть начинается при абсолютном нуле, но вместо градуса Цельсия использует градус Фаренгейта. Шкала имеет ограниченное применение и используется в основном в англоязычных странах для инженерных термодинамических расчётов.
Точке замерзания воды в этой шкале соответствует 491,67 °Ra, точке кипения воды – 671,67 °Ra . Разница между этими точками по шкале Рэнкина составляет 180 градусов (как и по шкале Фаренгейта).
Соотношение между градусами Рэнкина, Фаренгейта и кельвином: 1K = 1,8°Ra; t°Ra = t°F + 459,67 .
Формула для перевода градусов Рэнкина в градусы Цельсия и обратно:
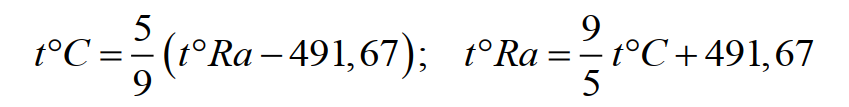 (21)
(21)
13. Лейденская шкала (лейденский градус °L или ÐL ) была введена в1957 году Х. ван Дийком и М. Дюро (шкала L55). Шкала, вероятно, восходит к 1894 году, к работам Хайке Камерлинг-Оннеса s52, который в 1897 году основал в Лейдене (Нидерланды) криогенную лабораторию. С начала XX века эта шкала использовалась для измерения криогенных температур ниже -183°C , то есть исходной точки в Международной температурной шкале тех времён, так как экспериментальная практика требовала измерений при более низких температурах. Таким образом, строго говоря, речь шла только о калибровке низкотемпературных косвенных измерений.
Шкала представляет собой шкалу Кельвина, смещенную таким образом, что за ноль градусов 0°L бралась температура кипения стандартного жидкого водорода ( -253°C ), состоящего на 75% из ортоводорода и на 25% из параводорода («нормальный» водород), а вторая реперная точка 70°L приблизительно соответствовала температуре кипения жидкого кислорода ( -183°C ). Абсолютный нуль равен -20,15°L .
После распространения Международных температурных шкал в область криогенных температур необходимость в лейденской шкале отпала.
Формула для перевода лейденских градусов в градусы Цельсия и обратно:
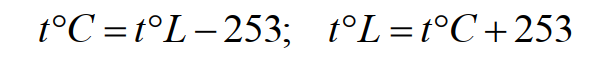 (22)
(22)
14. Следует также упомянуть о Планковской температуре, которая температурной шкалой не является, а показывает (как предполагается) максимально возможный предел абсолютных температур.
Планковская температура TP названа в честь немецкого учёного-физика Макса Планка и входит в планковскую систему единиц. Она представляет собой фундаментальный предел температуры в квантовой механике. В рамках нынешней физической теории считается, что выше планковской температуры энергия частиц становится настолько большой, что гравитационные силы между ними становятся сравнимы с остальными фундаментальными силами и понятие температурного взаимодействия теряет всякий смысл. В современной космологии предполагается, что таковой была температура Вселенной в первый момент (планковское время) Большого взрыва.
В планковской системе единиц Tp выражается через другие основные единицы этой системы, являющимися фундаментальными физическими постоянными:
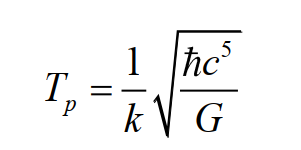 (23)
(23)
где c – скорость света, G – гравитационная постоянная, h— – постоянная Дирака (постоянная Планка h , делённая на 2π) и k – постоянная Больцмана.
В системы СИ планковская температура равна:
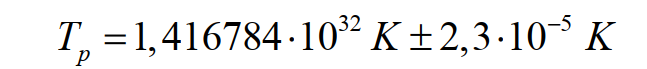 (24)
(24)
Поскольку Планковская температура – не шкала, а верхний предел, и также существует нижний предел, то есть абсолютный нуль температуры, любая температура может быть выражена в долях TP .
В заключение приведём сравнительную диаграмму наиболее важных температурных шкал
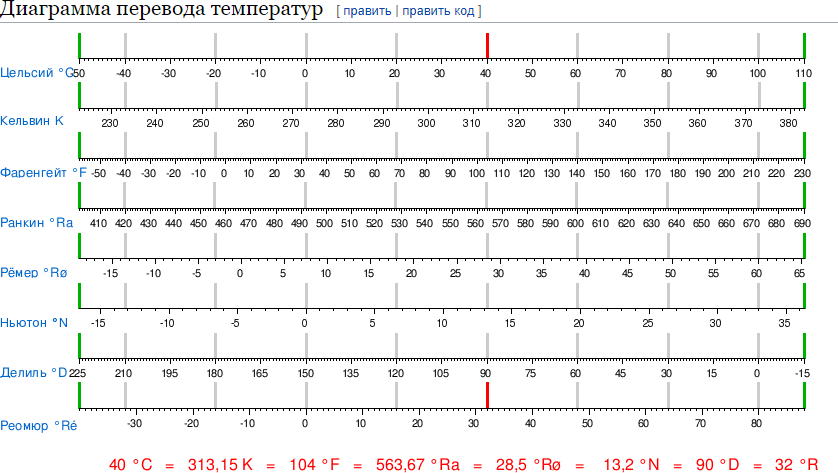
Рис. 18. Сравнительная диаграмма наиболее важных температурных шкал.